Момент силы и плечо силы

Дано определение момента силы и плеча силы. Определение плеча и момента силы рассмотрено на примерах ОДА человека при выполнении силовых упражнений.

Момент силы применительно к ОДА человека

Итак, мы познакомились с рычагом и узнали, что рычаг находится в равновесии (то есть неподвижен), если силы, приложенные к нему обратно пропорциональны их плечам.

F₂/F₁ = h₁/h₂

Это условие равновесия имеет один существенный недостаток – оно хорошо работает, если к рычагу приложены только две силы, однако сил может быть и больше. Чтобы преодолеть это препятствие, нужно ввести новую величину, которая называется момент силы.

Давайте представим условие равновесия рычага в следующем виде: F₁h₁ = F₂h_2.

Слева от этого равенства представлены показатели, которые характеризуют воздействие первой силы на рычаг, а справа – второй. Именно произведение силы на плечо силы и является величиной, которая называется моментом силы.

Определение момента силы

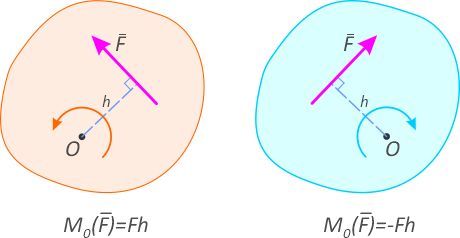
Момент силы относительно оси (М) – векторная величина, характеризующая меру вращательного действия силы. По своему значению момент силы относительно оси равен произведению силы на плечо силы:

М=F*h или Момент силы = сила*плечо силы.

Единица измерения момента силы – Ньютон х метр [Hм].

Момент силы считают положительным, если сила вызывает поворот тела против часовой стрелки, и отрицательным, при повороте тела по часовой стрелке.

Теперь давайте рассмотрим понятие плеча силы более подробно.

Определение плеча силы

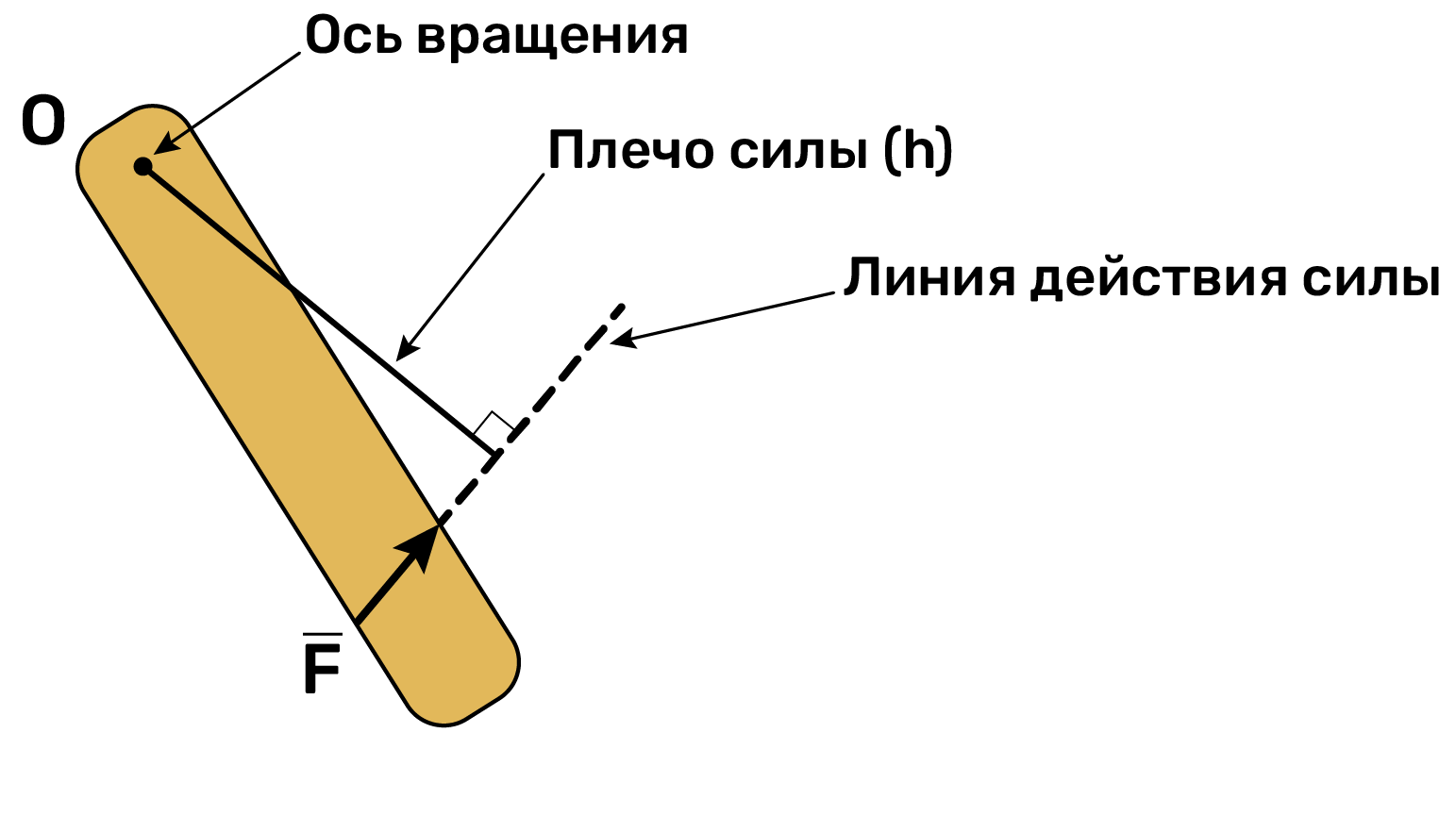
Плечо силы относительно оси (h) – это кратчайшее расстояние (длина перпендикуляра) от оси вращения (или центра вращения) до линии действия силы (Рис.1).
Линия действия силы — это прямая, вдоль которой направлен вектор действия силы (она имеет бесконечную длину в обе стороны).

Из определения плеча силы следует, что при прохождении линии действия силы через ось вращения, плечо силы равно нулю.

На рис.2. показаны два статических положения при выполнении жима штанги лежа: начальное (слева) и промежуточное (справа) в момент отрыва штанги от груди. Центром вращения является центр плечевого сустава. Плечо силы тяжести штанги относительно центра плечевого сустава в начальном положении (слева) равно нулю, потому что линия действия силы (она на рисунке показана штриховой линией) проходит через центр вращения (центр плечевого сустава). Плечо силы тяжести штанги в момент отрыва штанги от груди (справа) – это перпендикуляр, проведенный из центра вращения (центра плечевого сустава) до линии действия силы.

Рассмотрим еще одни пример. На рис.3. изображено статическое удержание гантели, закрепленной в области голеностопного сустава. Сила тяжести гантели представлена в виде вектора, направленного вертикально вниз. Линия действия силы тяжести представлена штриховой линией.

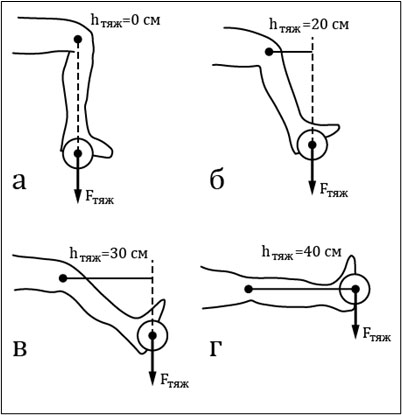
Плечо силы тяжести, соответствующее положению (рис. 3. а), равно нулю, так как линия действия силы проходит через ось вращения (центр коленного сустава). Плечо силы не является неизменным, а зависит от расположения голени относительно бедра. Максимальное значение плеча силы тяжести соответствует положению, изображенному на рис. 3.г. Именно это положение труднее всего удерживать длительное время.

Теперь рассчитаем значение момента силы тяжести относительно коленного сустава для положений, изображенных на рис.3. Давайте примем массу гантели равной 15 кг, то есть m = 15 кг, а плечи силы тяжести для положений а-г соответственно равными: а) h_тяж =0;  б) h_тяж = 15 см; в) h_тяж =30 см; г) h_тяж = 40 см. Массу голени в данном примере учитывать не будем.

Вначале определим значение силы тяжести гантели. Оно вычисляется по формуле и равно:

F_тяж = m*g = 15*9,8 = 147 H.

Напоминаю, что g – это ускорение свободного падения и оно равно 9,8 м/с².

Для случая а: момент силы тяжести гантели относительно оси, проходящей через центр коленного сустава будет равен нулю, так как плечо силы тяжести равно нулю.

Для случая б: M= F_тяж*h_тяж= 147*15= 2205 Н см

Для случая в: M= F_тяж*h_тяж= 147*30= 4410 Н см

Для случая г: M= F_тяж*h_тяж= 147*40= 5880 Н см

Таким образом, в положении г) сила тяжести гантели создает наибольший момент силы относительно центра коленного сустава. Удерживать гантель при полностью разогнутой ноге в коленном суставе значительно сложнее, чем при согнутой под углом в 90 градусов.

Главный момент силы

Если мы хотим учесть влияние момента, который создает сила тяжести, приложенная к голени и стопе относительно оси вращения, проходящей через центр коленного сустава (КС), необходимо определить главный момент силы относительно центра вращения в коленном суставе М_гл.

Главный момент силы (М_гл) равен алгебраической (то есть учитываются знаки моментов сил) сумме моментов силы тяжести голени (М_г, стопы (М_ст) и гантели (М_ган) относительно оси вращения, проходящей через центр коленного сустава (КС), то есть:

М_гл= М_г + М_ст + М_ган.

Чтобы пояснить метод расчета главного момента силы рассмотрим следующий пример.

Давайте рассчитаем для положения г (рис. 3г) значения главного момента силы тяжести относительно центра коленного сустава, учитывая массу голени, стопы и гантели. Массу голени примем равной  5 кг, то есть m_г = 5 кг, плечо силы тяжести голени примем равным 20 см, то есть h_г = 20 см; примем массу стопы равной 2 кг, то есть m_ст = 2 кг, а плечо силы тяжести стопы примем равным 35 см, то есть h_ст = 35 см; массу гантели примем равной 15 кг, то есть m_ган = 15 кг, плечо силы тяжести гантели примем равным 40 см, то есть h_ган = 40 см

Тогда:

Момент силы тяжести голени равен:M_г=F_г* h_г= 5*9,8*20 = 980 Hсм

Момент силы тяжести стопы равен: M_ст=F_ст* h_ст=2*9,8*35= 686 Нсм.

Момент силы тяжести гантели равен: M_ган=F_ган* h_ган= 15*9,8*40 = 5580 Нсм.

Главный момент силы тяжести системы «голень-стопа-гантель» равен:

М_гл = М_г + М_ст + М_ган = 980 + 686+ 5580 = 7546 Нсм.

(Правильнее было бы написать, что Мгл = -7546 Нсм, так как все силы создают момент силы по часовой стрелке, но так как при расчете главного момента не было сил, создающих положительный момент, я использовала абсолютные величины моментов).

Изменение главного момента силы тяжести рассмотрим на следующем примере (рис.4).

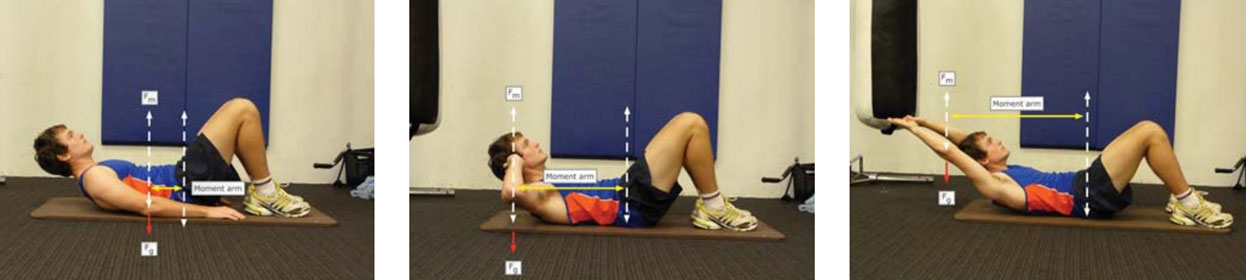
Вы хорошо знаете, что выполнение упражнения, показанного на рисунке 4 легче всего выполнять, когда руки вытянуты вдоль туловища (то есть приближены к центру вращения, в данном случае это центр тазобедренного сустава). Наиболее сложно выполнять это упражнение, когда руки вытянуты за голову. Почему это происходит?  Дело в том, что положение рук изменяет главный момент силы тяжести. Главный момент силы тяжести – это сумма момента силы тяжести туловища, момента силы тяжести головы и момента силы тяжести рук. Моменты силы тяжести туловища и головы во всех трех положениях одинаковы, а момент силы тяжести рук меняется. Он тем больше, чем дальше центр тяжести рук расположен от центра вращения (в данном случае тазобедренного сустава), то есть больше плечо силы тяжести рук. Так как мышцам пресса и сгибателям бедра нужно противодействовать большему моменту силы тяжести, когда руки вытянуты за головой, то и выполнять это упражнение значительно сложнее.

Литература

1. Бегун П.И., Самсонова А.В. Биомеханика опорно-двигательного аппарата человека. – Монография. – СПб: Кинетика, 2020.- 179 с.
2. Энока Р. Основы кинезиологии. Киев: Олимпийская литература, 1998. – 399 с.
3. Keogh J.W.L., Lake J.P., Swinton P.A.  Practical Applications of Biomechanical Principles in Resistance Training: Moments and Moment Arms // Journal of Fitness Research, 2013.– Vol. 2.– N. 2. – P.39-48.

С уважением, А.В.Самсонова