Закон Гука
Дано описание жизни и открытий Роберта Гука. Подробно рассмотрен закон Гука, его применимость и примеры расчета силы упругости, возникающей в деформированном теле, на основе этого закона. Приведены значения коэффициента жесткости пружины и мышц-сгибателей стопы.
Закон Гука (закон упругих деформаций)
Прежде чем мы разберемся, что представляет собой закон Гука несколько слов об его авторе – Роберте Гуке.
Роберт Гук (жизнь и открытия)
Роберт Гук (Robert Hook, 1635-1703) – один из выдающихся английских ученых и изобретателей. Он успешно проявил себя в самых разных областях науки того времени: механике, оптике, астрономии, архитектуре, биологии и поэтому получил прозвище «английского Леонардо да Винчи», рис.1.

Мы все знаем его как ученого, установившего зависимость между силой упругости, возникающей при растяжении или сжатии пружины и её удлинением. Но есть и более серьезные открытия Роберта Гука. Роберт Гук одним из первых подошел к открытию закона притяжения тел.
В работе «Попытка изучения движения Земли», вышедшей в свет в 1674 году он писал: » Я разовью теорию, которая во всех отношениях согласуется в общепризнанными правилами механики. Теория эта основывается на трех допущениях: во-первых, что все без исключения небесные тела обладают направленным к их центру притяжением или тяжестью, благодаря которой они притягивают не только свои собственные части, но также и все находящиеся в сфере их действия небесные тела. Согласно второму допущению все тела, движущиеся прямолинейно и равномерным образом, будут двигаться по прямой линии до тех пор, пока они не будут отклонены какой-нибудь силой и не станут описывать траектории по кругу, эллипсу или какой-нибудь менее простой кривой. Согласно третьему допущению силы притяжения действуют тем более, чем ближе к ним находятся тела, на которые они действуют» (цит. по В. Григорьев, Г. Мякишев, 1977).
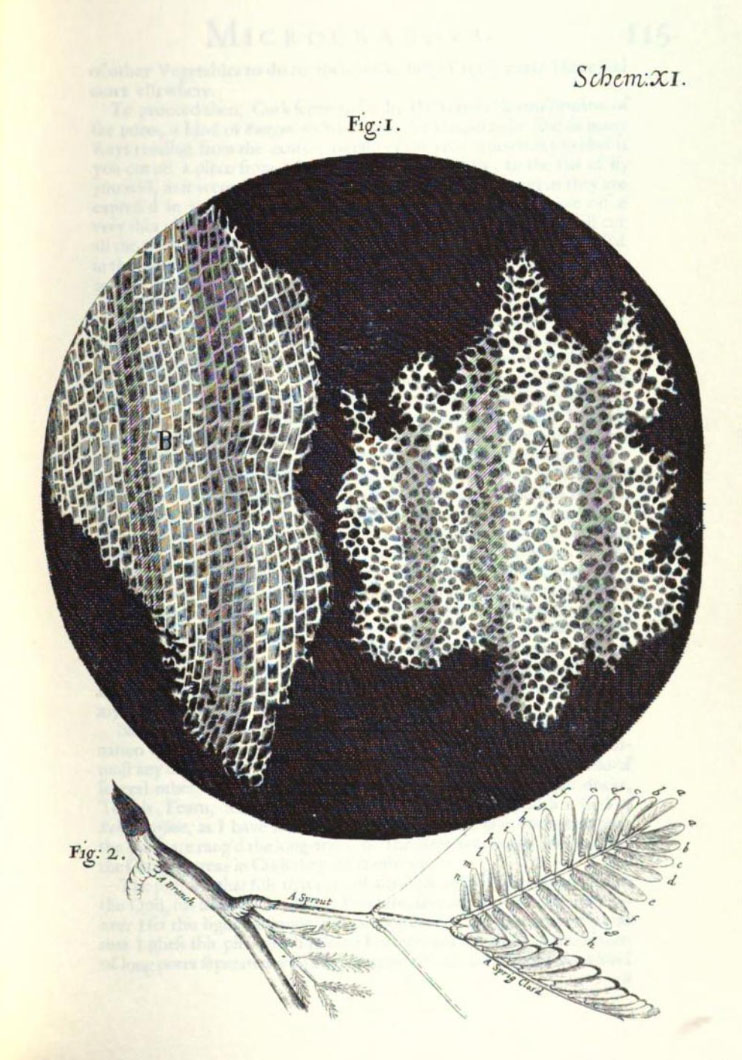
Не менее важное открытие произведено Робертом Гуком в области биологии. Он установил, что ткани живых организмов, состоят из структурных единиц, которые он назвал клетками (Cells). Свои результаты исследования строения растений и животных посредством усовершенствованного микроскопа, Роберт Гук изложил в книге Micrographia, изданной в 1665 году. Эта книга снабжена прекрасными рисунками, ведь Роберт Гук очень хорошо рисовал (рис. 2). Однако перейдем к закону упругих деформаций.
Закон Гука
В 1660 году, в возрасте 25 лет Роберт Гук открыл закон, носящий теперь его имя. Этот закон в современной трактовке звучит так:
«Сила упругости, возникающая при растяжении или сжатии тела, пропорциональна его удлинению».
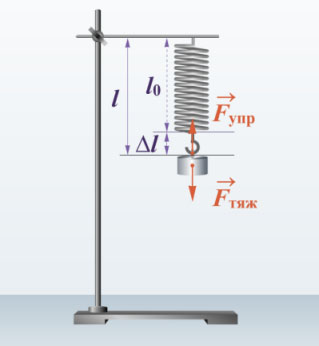
Впервые Гук записал это открытие в виде анаграммы «ceiiinosssttuv», расшифровку которой он опубликовал в 1678 году в следующем виде «Ut tensio, sic vis («Каково растяжение, такова и сила»). В результате произведенного открытия Роберт Гук разработал пружину, которая позволила портативному хронометру (часам) показывать время более точно, потому что сила упругости, возникающая внутри пружины прямо пропорциональна её растяжению. Согласно третьему закону Ньютона сила (F), c которой растягивают пружину, равна силе упругости Fупр, но направлена в противоположную сторону (рис. 3).
Закон Гука можно записать в следующем виде:
Fупр= k • Δl (1),
где:
- Fупр — сила упругости;
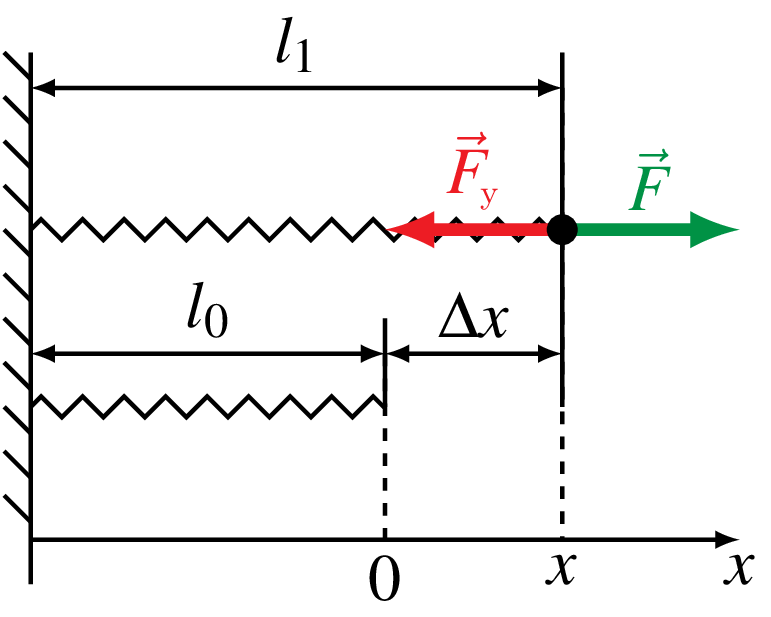
- Δl — абсолютное удлинение (сжатие) тела, равное Δl = l1 — l0;
- k — коэффициент жесткости (упругости) пружины.
Коэффициент жесткости тела
В формуле (1) имеется коэффициент пропорциональности (k), связывающий силу упругости с абсолютным удлинением (сжатием) тела. Коэффициент жесткости для различных тел зависит не только от свойств материала, но и от формы тела и его геометрических размеров.
Коэффициент жесткости пружины
Например, коэффициент жесткости витой цилиндрической пружины зависит от свойств материала, диаметра проволоки, диаметра витка пружины и количества витков. Этот показатель пружин различных типов варьирует в очень широких пределах от 4000 (сверхлегкая нагрузка) до 100000 Н/м (сверхтяжелая нагрузка) для пружин сжатия, а для пружин растяжения — от 2000 (сверхлегкая нагрузка) до 800000 Н/м (сверхтяжелая нагрузка).
Коэффициент жесткости тонкого упругого стержня
Как было показано выше, коэффициент жесткости зависит как от свойств материала, так и от формы тела и его размеров. Для тонкого упругого стержня, коэффициент жесткости будет равен:
k = (Е•S)÷l (2),
где:
- Е — модуль Юнга — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации.
- S — площадь поперечного сечения стержня;
- l — длина стержня.
Если ввести относительное удлинение (ε)
ε=Δl÷l (3),
и нормальное напряжение (σ) в поперечном сечении стержня, равное:
σ = F ÷ S (4),
Закон Гука для тонкого растяжимого стержня может быть записан в следующем виде:
σ = E • ε (5).
Коэффициент жесткости для мышц-сгибателей стопы
Коэффициент жесткости мышц сгибателей стопы у спортсменов — представителей различных видов спорта сильно варьирует. У бегунов-спринтеров он составляет ≈ 30000 Н/м, а у футболистов — ≈ 24700 Н/м.
Область применимости закона Гука
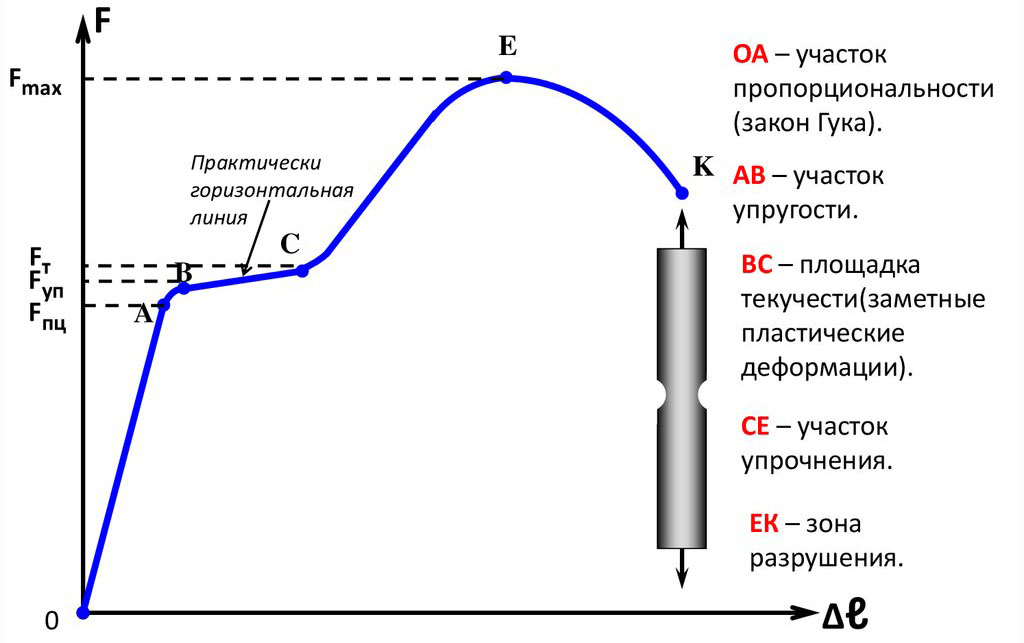
Следует отметить, что закон Гука выполняется только для упругих деформаций, то есть для деформаций, которые исчезают при устранении внешней силы, вызвавшей деформацию. На рис.4 приведена диаграмма растяжения образца (тонкого стержня из пластичного материала, например, из стали). Из рис. 4 следует, что только на участке ОA выполняется закон Гука. То есть на участке ОА образец испытывает упругую деформацию. В дальнейшем на участке графика ВК закон Гука нарушается, наблюдается нелинейная деформация образца.
Литература
- Боголюбов А.Н. Роберт Гук (1635-1703).- М.: Наука, 1984.
- Hooke Robert Micrographia: Or Some Physiological Descriptions of Minute Bodies Made by Magnifying Glasses, with Observations and Inquiries Thereupon. (1665) The Royal Society.
- Григорьев В., Мякишев Г. Силы в природе.- М.:Наука, 1977.- 415 с.
С уважением, А.В. Самсонова