Нормальный закон распределения (закон нормального распределения)

Нормальный закон распределения случайной величины (закон нормального распределения)

Значение для исследований в области физической культуры и спорта (ФКиС)

Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основополагающую роль в математической статистике. Причинами это являются:

1. Многие эмпирические распределения можно успешно описать с помощью нормального закона распределения. Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
2. Нормальное распределение обладает рядом благоприятных математических свойств, обеспечивших его широкое применение в статистике.
3. Корректное использование критериев проверки статистических гипотез предполагает знание закона распределения экспериментальных данных. Так, например, использование t – критерия Стьюдента и  F-критерия Фишера требует нормального распределения экспериментальных данных.
4. Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения.

Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.

История изучения нормального распределения

Блез Паскаль и Пьер Ферма

Первые исследования по теории вероятностей проводили математик, механик, физик Блез Паскаль и математик Пьер Ферма в середине XVII века. Эти исследования выполнялись по  просьбе Шевалье де Мере, азартного игрока в кости, который пытался понять природу выигрыша. В дальнейшем эти исследования заложили основы теории вероятностей (Дж. Гласс, Дж. Стэнли, 1976).

Якоб Бернулли

Дальнейшее развитие теория вероятностей получила в XVIII веке в трудах швейцарского математика Якоба Бернулли (рис.1). В 1713 году была опубликована  его книга  «Искусство предположений».

В этой книге был рассмотрен ряд вопросов теории вероятностей.  Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также  дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).

Якобу Бернулли принадлежит формула подсчёта вероятности появления события A  определенное  количество раз при любом числе независимых испытаний (рис. 2)

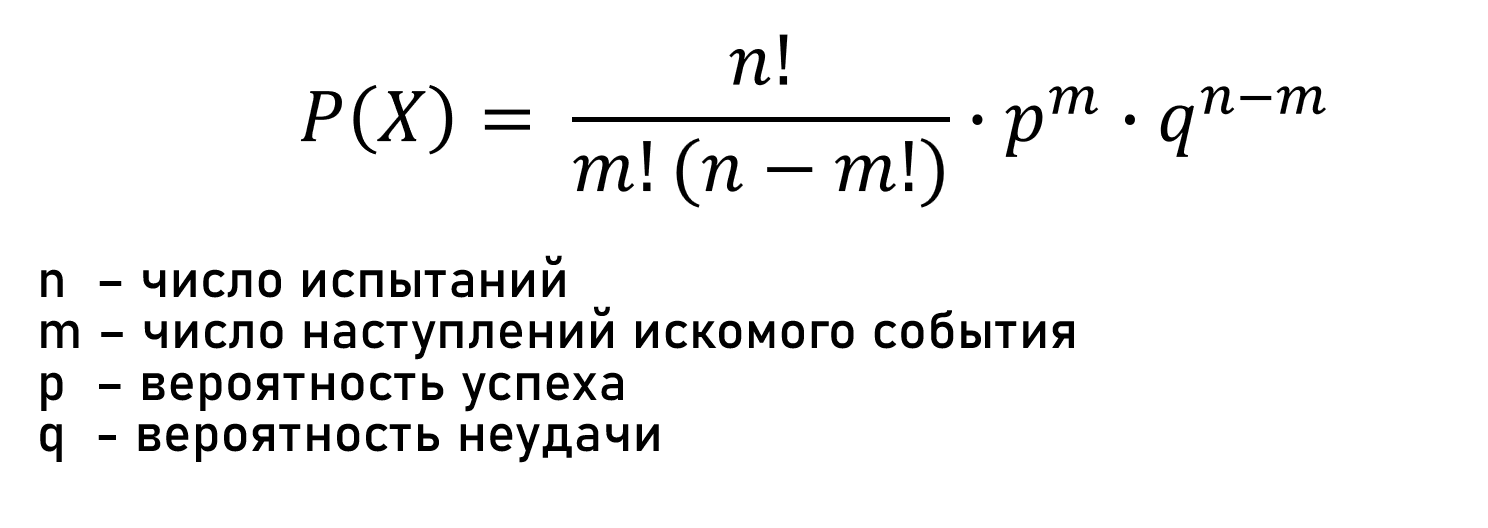
Джеймс Стирлинг

В последствии (в 1730 г.) шотландский математик Джеймс Стирлинг опубликовал формулу, аппроксимирующую произведение первых n чисел. Это позволило упростить решение ряда задач, которые встречаются в теории вероятностей. Однако все еще эти задачи оставались трудно разрешимыми.

Абрахам де Муавр

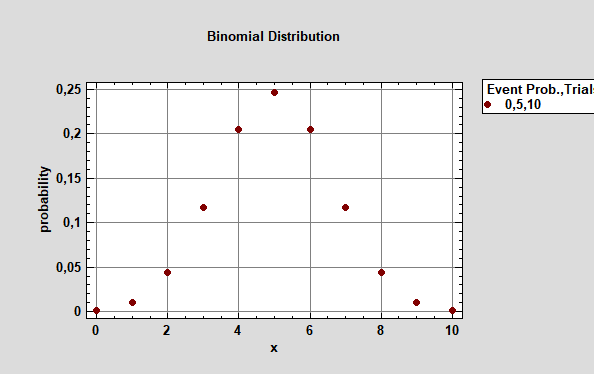
Эту задачу решил английский математик Абрахам де Муавр (рис.3). В работе «Доктрина случайностей», которая была издана в 1738 году он привел формулу, аппроксимирующую  биномиальное распределение события, вероятность которого была равна 0,5  (рис.4).  То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 4. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление  формулы нормального распределения значительно упростило расчеты вероятностей событий.

Пьер-Симон де Лаплас

В 1783 году французский математик, механик, физик и астроном Пьер-Симон де Лаплас (рис. 5)  использовал нормальную кривую для описания распределения ошибок. Затем, в начале XIX века (в 1812 г.) французский математик, механик, физик и астроном Пьер-Симон де Лаплас  обобщил результаты А. Муавра для произвольного биномиального распределения в книге «Аналитическая теория вероятностей» (Théorie analytique des probabilités).

Карл Фридрих Гаусс

Одновременно с П. Лапласом в 1809 году немецкий математик, механик, физик и астроном Карл Фридрих Гаусс (рис. 6) в сочинении «Теория движения небесных тел» использовал формулу нормального распределения для описания случайных ошибок, возникающих в результате многократных измерений  движений небесных тел. К.Ф. Гаусс внес настолько большой вклад в разработку теории нормального распределения, что впоследствии это распределение стали назвать гауссово распределение или распределение Гаусса-Лапласса.

Адольф Кетле

В начале ХХ века бельгийский математик, астроном и социолог Адольф Кетле  (рис.7) одним из первых применил  нормальный закон распределения случайной величины к анализу биологических и социальных процессов.

Изучая распределение солдат американской армии по росту, Адольф Кетле  обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1835).

В настоящее время нормальное распределение широко используется в биологии, медицине, экономике и других областях науки.

Формула нормального распределения

Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:

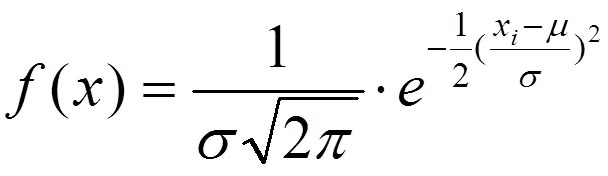
где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.

Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0  и σ=1.  Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. График функции плотности вероятностей нормального распределения вероятностей имеет вид (рис.8).

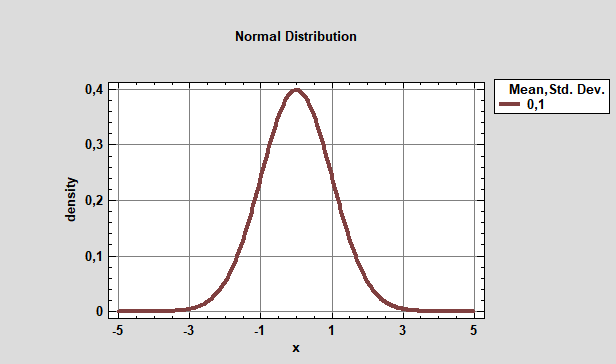
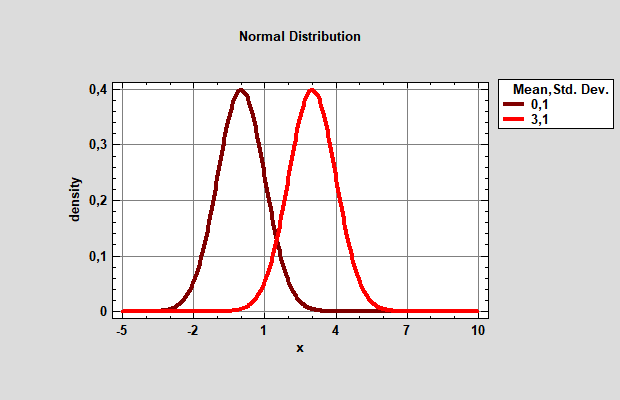
Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при  μ=3 график сместится вправо вдоль оси Х  (рис.9).

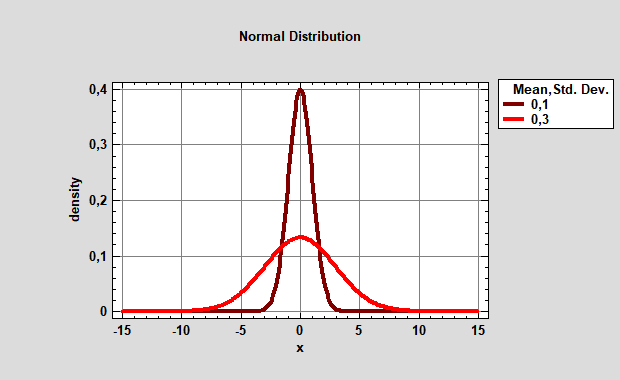
Если мы оставим μ=0 , а изменим параметр σ, например σ=3, то получим распределение с большим размахом (рис.10).

Свойства нормального распределения

1. Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
2. Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
3. Медиана и мода нормального распределения совпадают и равны µ.
4. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.

Нормированное отклонение

В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:

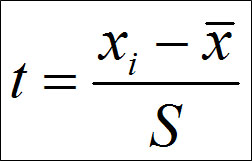
Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.

Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».

Нормированное нормальное распределение

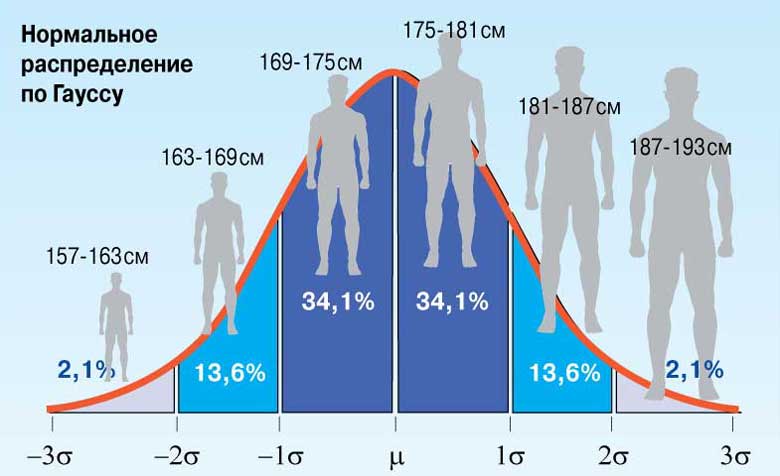
Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.

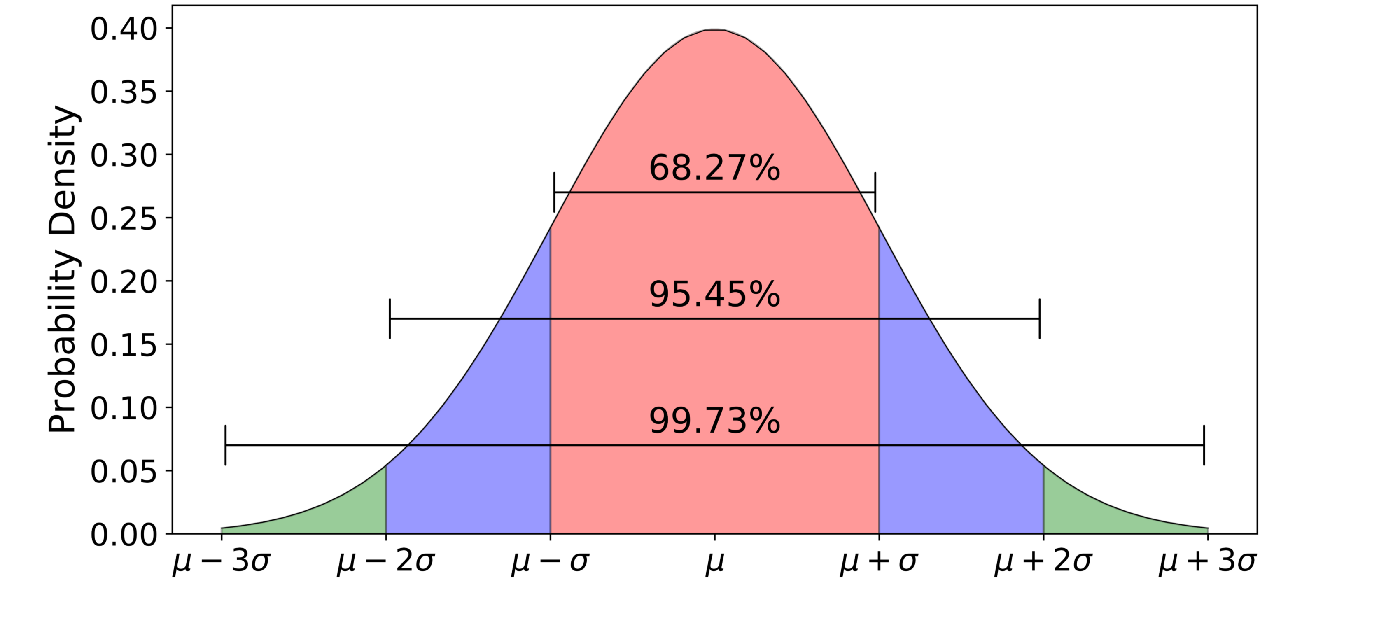
Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры:   µ=0; σ = 1 (рис.8, 11). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле: U= (X-μ)/σ.

Для нормированного нормального распределения характерно, что в интервал µ±σ попадают 68 % всех результатов, в интервал µ±2σ попадают 95% всех результатов, в интервал µ±3σ попадают 99 % всех результатов.

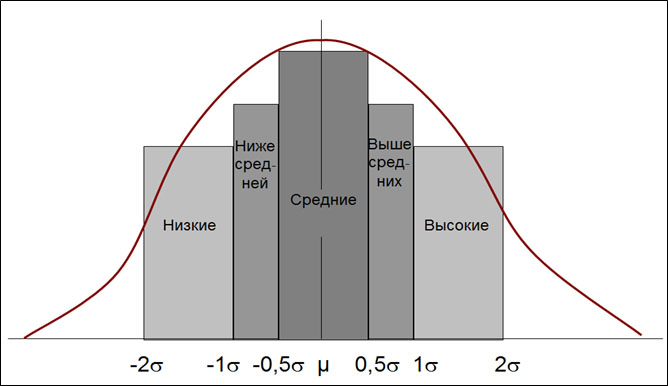
В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М. Зациорским (рис. 12) предложено использовать следующую систему оценок результатов.  Если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.

Критерии согласия

Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.

Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).

Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:

• если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки;
• если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова.
• в статистическом пакете Statgraphics Centurion существует специальная опция — критерии проверки нормальности распределения. В этой опции есть четыре критерия, посредством которых можно сделать вывод о соответствии эмпирического распределения нормальному закону.

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии.- М.: Прогресс, 1976.-495 с.
3. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
4. Кетле А. (1835) Социальная физика, или опыт исследования о развитии человеческих способностей.  Т.1, 1911.- С. 38-39.
5. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
6. Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.

С уважением, А.В. Самсонова