Точечное и интервальное оценивание числовых характеристик выборки
Точечной оценкой числовой характеристики выборки называют оценку, которая определяется одним числом. К точечным оценкам относятся: среднее арифметическое, дисперсия или стандартное отклонение.
Например, статистическая обработка результатов 50 спортсменов в беге показал, что среднее арифметическое времени пробегания 100 м равно 15,38 с. Это число является точечной оценкой среднего арифметического.
Если выборка небольшого объёма, то точечная оценка может значительно отличаться от оцениваемого параметра генеральной совокупности, в данном случае от среднего арифметического генеральной совокупности (обозначается μ) и её использование может привести к грубым ошибкам. Поэтому при небольшом объёме выборки в математической статистике используют другого типа оценки характеристик генеральной совокупности – интервальные.
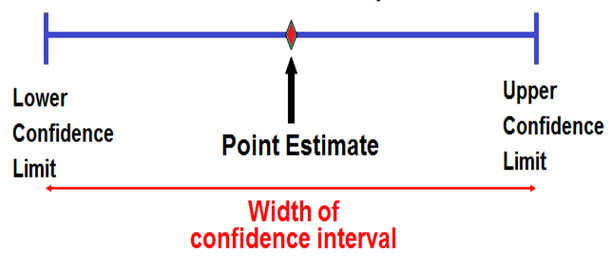
Интервальной оценкой числовой характеристики называется интервал[1], который с доверительной вероятностью P (задаваемой заранее) накрывает истинное значение числовой характеристики генеральной совокупности.
Как правило, в научных исследованиях в области физической культуры и спорта считается достаточной доверительная вероятность Р=0,95. В некоторых случаях, связанных с большой ответственностью при принятии решений, принимают P равной 0,99 или 0,999. Таким образом, доверительная вероятность – это уровень гарантии суждения о значениях генеральной характеристики на основании выборочных данных.
Вероятность α=1-Р того, что построенный доверительный интервал не накроет значение генеральной характеристики, называется уровнем значимости; другими словами, α — вероятность ошибки.
В литературе часто обе вероятности α и P выражают в процентах, т.е. 100α% и 100P%.
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта (электронная книга)
- Математическая статистика в спортивных исследованиях (электронная книга)
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
Для определения доверительного интервала необходимо знать значение параметра t. Он зависит от объема выборки (n) и доверительной вероятности P (таблица 1).
Таблица 1 — Значения t в зависимости от объёма выборки и доверительной вероятности Р.
| n | Р | ||
| 0,95 | 0,99 | 0,999 | |
| 10 | 2,265 | 3,250 | 4,781 |
| 15 | 2,145 | 2,977 | 4,140 |
| 20 | 2,093 | 2,861 | 3,883 |
| 30 | 2,042 | 2,750 | 3,646 |
| 40 | 2,021 | 2,704 | 3,551 |
| 50 | 2,009 | 2,678 | 3,505 |
| 60 | 2,000 | 2,660 | 3,505 |
| 80 | 1,990 | 2,639 | 3,416 |
Покажем на примере, как определить границы 95% доверительного интервала для среднего результата в беге на 100 м (n = 50), если: среднее арифметическое равно 15,38 с, а стандартная ошибка среднего арифметического равна 0,13 с.
Из таблицы 1 для n = 50 и P= 0,95 находим значение t. Оно равно t=2,009. Следовательно, доверительный интервал будет следующим: 15,38 — 2,009·0,13<μ<15,38+2,009·0,13
или 15,12<μ<15,64 с
После округления получим итоговый результат: 15,1<μ<15,6 c
Таким образом, с доверительной вероятностью Р=0,95 можно утверждать, что генеральное среднее μ заключено в границах от 15,1 до 15,6 с.
Если мы хотим с большей вероятность (например, Р=0,99) утверждать, что генеральное среднее заключено в определенном интервале, необходимо из таблицы 1 найти значение t для n = 50 и P= 0,99. Оно равно t=2,678.
Тогда доверительный интервал для генерального среднего арифметического будет следующим:
15,38 — 2,678·0,13<μ<15,38+2,678·0,13
или 15,03<μ<15,73 с.
После округления получим итоговый результат: 15,0<μ<15,7 c.
Таким образом, с доверительной вероятностью Р=0,99 можно утверждать, что генеральное среднее μ заключено в границах от 15,0 до 15,7 с. То есть утверждение с большей вероятностью увеличивает интервал, в котором заключено генеральное среднее арифметическое.
Литература
- Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.
С уважением, А.В. Самсонова
[1] Интервал – множество всех чисел, удовлетворяющих строгому неравенству a < x < b
- Учебные пособия по статистике
- Видеоуроки по Statgraphics
- Введение в математическую статистику
- Генеральная совокупность и выборка
- Статистические шкалы
- Эмпирические распределения
- Числовые характеристики выборки
- Стандартная ошибка среднего арифметического
- Представление результатов исследования
- Точечное и интервальное оценивание числовых характеристик
- Элементы теории вероятностей
- Нормальный закон распределения (закон нормального распределения)
- Статистические гипотезы
- Критерии проверки статистических гипотез
- Критерии согласия
- Обоснование выбора критерия значимости
- Параметрические критерии
- Статистические операции в номинальной шкале
- Представление данных статистического анализа
- Корреляционный анализ
- Представление данных корреляционного анализа
- Регрессионный анализ
- Представление результатов регрессионного анализа