Применение статистических шкал в области науки и практики
Введение
Грамотное применение статистических методов обработки данных во многом зависит от четкого понимания исследователем того, в какой статистической шкале они представлены. Непонимание этого может привести к тому, что исследователь получит результаты, которые не отражают действительное положение вещей и сделает неправильные выводы. Именно поэтому необходимо знать, в какой шкале представлены статистические данные.
Классификация данных
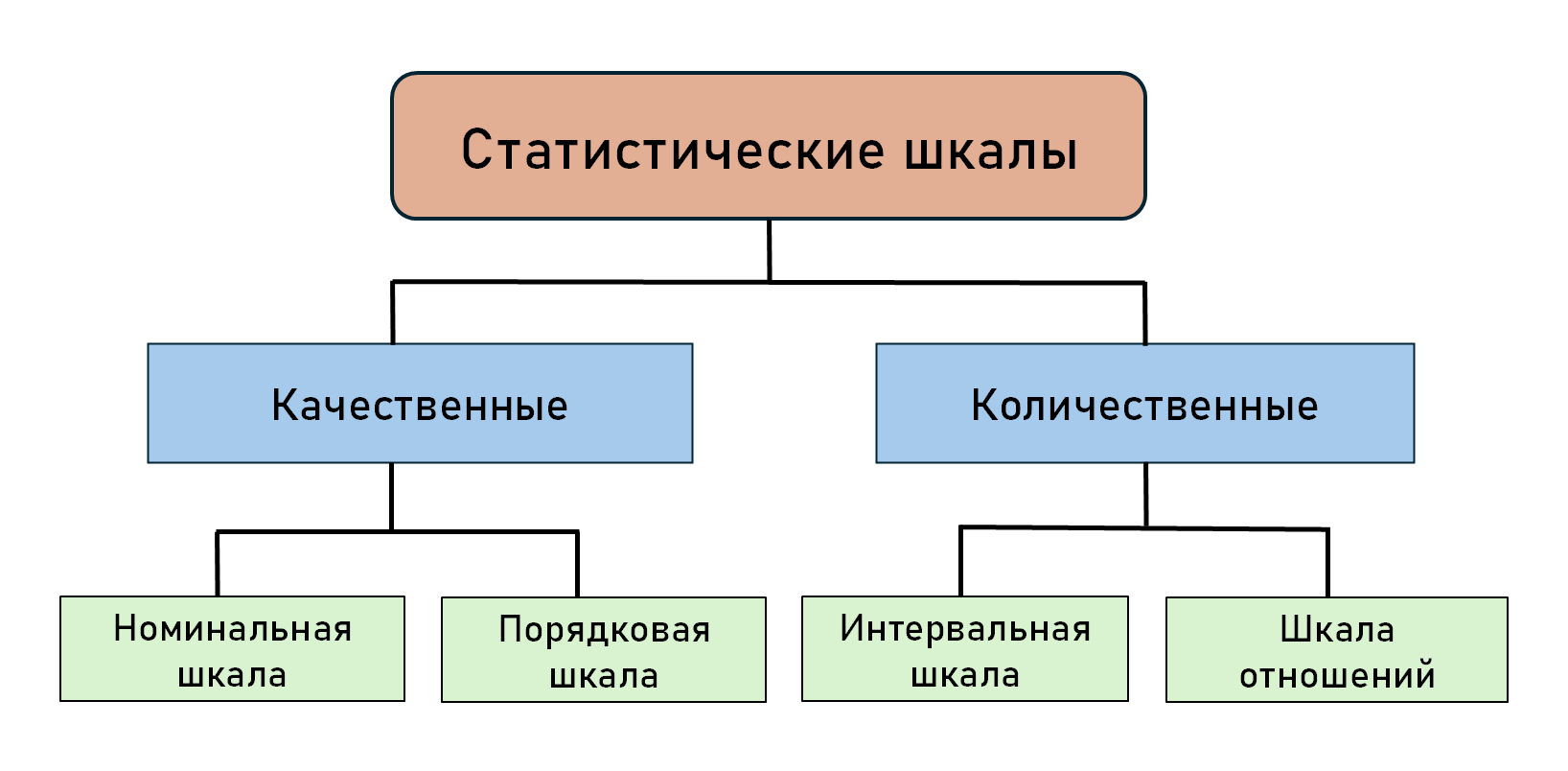
Прежде чем перейти к статистическим шкалам необходимо знать классификацию исходных данных. Эти данные (переменные) подразделяются на номинативные, ранговые (порядковые), дискретные и непрерывные. Номинативные и ранговые относятся к качественным данным, а дискретные и непрерывные — к количественным.
Теперь разберемся, что представляют собой статистические шкалы.
Определение статистической шкалы
Шкала (от лат. «скале» — лестница) – элемент счетной системы, посредством которого происходит отнесение исследуемого объекта к определенной группе объектов.
Типы шкал
Статистические шкалы можно разделить на качественные и количественные. К качественным шкалам относится номинальная и порядковая шкалы. К количественным – интервальная шкала и шкала отношений (рис.1).
Номинальная шкала
Номинальная шкала (Nominal) – качественная шкала. Относится к самому элементарному типу измерения. В ней каждому оцениваемому объекту приписывается наименование или число.
Пример 1: Признак – пол. Цифрой «0» обозначаем женщин, цифрой «1» — мужчин. Очевидно, что расчет среднего арифметического не имеет смысла.
Пример 2: Признак — Цвет волос: Цифрой «1» обозначаем брюнетов, цифрой «2» — шатенов, цифрой «3» – блондинов, цифрой «4» – людей, имеющих рыжий цвет волос.
Пример 3: Номера на футболках спортсменов (рис.2).

- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта (электронная книга)
- Математическая статистика в спортивных исследованиях (электронная книга)
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
В области физической культуры и спорта, психологии и медицины часто используется метод анкетного опроса. При этом результаты представлены в виде таблицы, в которой представлена абсолютная частота ответов на тот или иной вопрос (табл. 1). Такие данные также можно отнести к номинальным.
С данными, представленными в номинальной шкале возможны следующие статистические операции: частотный анализ, а также проверка статистических гипотез с использованием следующих критериев: хи-квадрата, точного критерия Фишера, критерия МакНемара и углового преобразования Фишера.
Таблица 1 — Влияние занятий спортом студентов технических вузов на утомляемость после рабочего дня (n=200) (В.С. Иванов, 1990)
Утомляемость | Занятия спортом | |
| Да | Нет | |
| Да | 36 | 124 |
| Нет | 28 | 12 |
| Всего | 64 | 136 |
Порядковая шкала
Порядковая шкала (ранговая, Ordinal) – качественная шкала, использующая свойство чисел отражать отношение «больше – меньше».
Так, например, различные сорта перцев можно расположить в порядке возрастания их остроты и присвоить им числа: 1 — острый; 2 — более острый; 3 — жгучий (рис.3).

В порядковой шкале нельзя сказать насколько или во сколько одно значение больше другого, но можно сказать какое больше, какое меньше. Очень часто статистические данные, представленные в порядковой шкале, измеряются в баллах.
В области физической культуры и спорта в баллах измеряются результаты в спортивной и художественной гимнастике; в фигурном катании; в прыжках в воду; в прыжках на лыжах с трамплина; в фристайле (лыжной акробатике).
Также примером порядковой шкалы является шкала Мооса, которая используется для определения твердости минералов. Она содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10 (рис.4).
Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) — не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно.

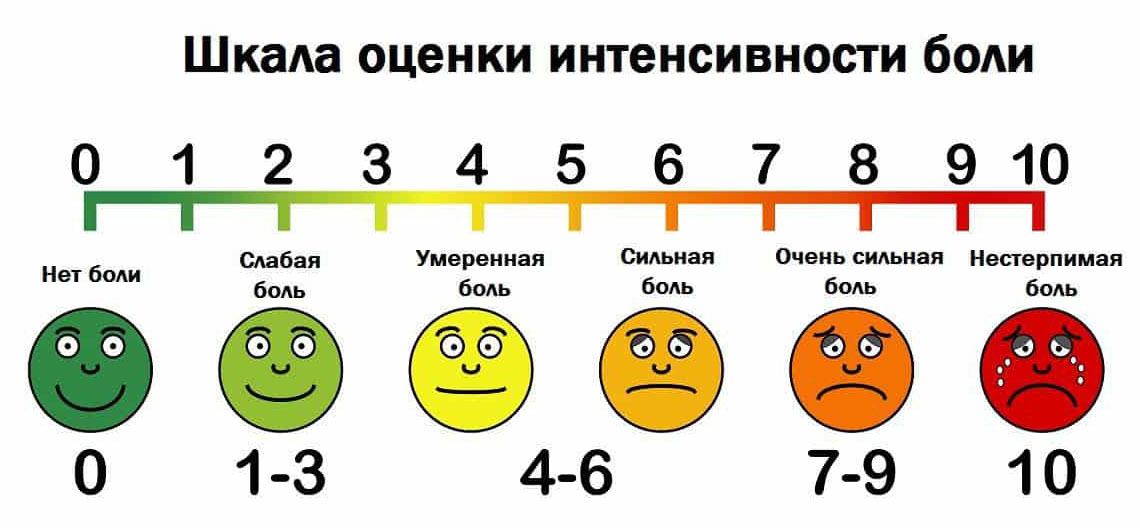
Еще одним примером порядковой шкалы является Faces Pain Scale – Международная шкала измерения боли по выражению лица (применяется в педиатрии), рис. 5.
Еще одним примером порядковой шкалы является шкала, предложенная Ренсисом Лайкертом в 1930-х годах. Она представляет собой широко используемую оценочную шкалу, которая требует от респондентов указать степень согласия или несогласия с каждым из серии утверждений об объектах-стимулах.
Пример шкалы Лайкерта
Оцените свое психическое состояние:
- Крайне неустойчивое
- Неустойчивое
- Устойчивое
- Очень устойчивое
В порядковой шкале допускаются следующие статистические операции:
- Частотный анализ (расчет частот).
- В качестве характеристик положения — расчет медианы (Ме).
- В качестве характеристик вариативности – расчет квантилей.
- В качестве меры независимости двух признаков — расчет критериев Манна-Уитни и Вилкоксона.
- В качестве меры связи двух признаков – расчет рангового коэффициента корреляции (Спирмена).
Интервальная шкала
Интервальная шкала (Interval) – количественная шкала. В этой шкале устанавливается объективная единица измерения. Однако нулевое значение устанавливается субъективно.
В интервальной шкале, например, измеряется температура тела. Шкала температуры тела по Цельсию за ноль градусов принимает температуру таяния льда, а за 100 — температуру кипения воды. Шкала температуры тела по Фаренгейту за ноль градусов принимает температуру смеси воды, льда и хлорида аммония, а за 96 град — температуру тела здорового человека, рис.6.
Также примером интервальной шкалы является настоящее летосчисление (за ноль принят год рождения Иисуса Христа).

Шкала отношений
Шкала отношений (Ratio) — количественная шкала. В этой шкале, как и в интервальной шкале имеется объективная единица измерения. Нулевое значение устанавливается объективно и означает полное отсутствие признака. Для признаков, измеренных в шкале отношений можно дополнительно сказать: во сколько одно значение больше другого.
Примерами статистических данных, представленных в шкале отношений являются признаки: рост, вес, температура по Кельвину (за ноль принято состояние тела, соответствующее минимальной теоретически возможной внутренней энергии тела), результаты в беге (рис. 7), в прыжках в длину, толкании ядра и др.

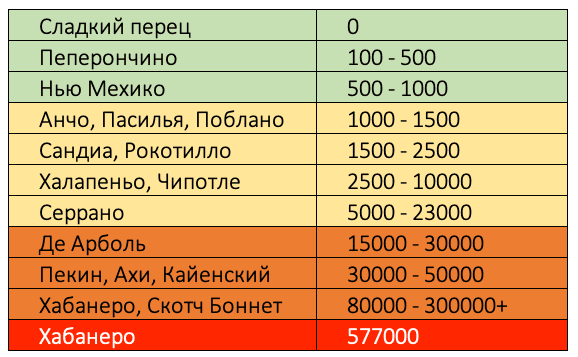
Также примером шкалы отношений является шкала Сковилла — американского ученого-химика, профессора Массачусетского колледжа Уилбура Сковилла. Во время работы в фармацевтической компании Parke-Davis, Уилбур Сковилл решил измерить степень остроты различных сортов перцев с целью возможного её применения при тестировании лекарственных препаратов. За единицу измерения У.Сковилл предложил взять удельный вес капсаицина в перце. Данную единицу он назвал единицей шкалы Сковилла (ЕШС) или SHU в международной системе единиц. За точку отсчета (то есть за нулевое значение) химик взял остроту сладкого болгарского перца, так как, в его составе капсаицина практически нет. Максимальной степенью остроты обладает перец сорта Хабанеро — 577000 (рис. 8).
С данными, представленными в интервальной шкале и шкале отношений возможны все статистические операции. Более подробное эта тема рассмотрена в литературе, ссылки на которую приведены ниже.
Литература
- Барникова, И.Э. Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта: учеб. пособие / И.Э. Барникова; А.В. Самсонова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт–Петербург. – СПб.: [Б.и.], 2017. – 103 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.
С уважением, А.В.Самсонова
- Учебные пособия по статистике
- Видеоуроки по Statgraphics
- Введение в математическую статистику
- Генеральная совокупность и выборка
- Статистические шкалы
- Эмпирические распределения
- Числовые характеристики выборки
- Стандартная ошибка среднего арифметического
- Представление результатов исследования
- Точечное и интервальное оценивание числовых характеристик
- Элементы теории вероятностей
- Нормальный закон распределения (закон нормального распределения)
- Статистические гипотезы
- Критерии проверки статистических гипотез
- Критерии согласия
- Обоснование выбора критерия значимости
- Параметрические критерии
- Статистические операции в номинальной шкале
- Представление данных статистического анализа
- Корреляционный анализ
- Представление данных корреляционного анализа
- Регрессионный анализ
- Представление результатов регрессионного анализа
