Статистические гипотезы

Статистические гипотезы (их виды и ошибки при проверке)

Определение

 Статистической гипотезой (гипотезой) называется любое утверждение об изучаемом законе распределения или характеристиках случайных величин.

Пример статистических гипотез:

1. Генеральная совокупность распределена по нормальному закону.
2. Дисперсии двух нормально распределенных совокупностей равны между собой.

Виды статистических гипотез

Нулевая гипотеза (Н₀) — предположение о том, что между  параметрами генеральных совокупностей нет различий, то есть эти различия носят не систематический, а случайный характер.

Пример 1. Нулевая гипотеза записывается следующим образом:

H₀: µ₁=µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности равно генеральному среднему другой совокупности).

 Альтернативная гипотеза (Н₁) – предположение о том, что между параметрами генеральных совокупностей есть достоверные различия.

 Пример 2. Альтернативные гипотезы записываются следующим образом:

• H₁: µ_1≠µ₂ (альтернативная гипотеза заключается в том, что генеральное среднее одной совокупности не равно генеральному среднему другой совокупности).
• H₁: µ₁>µ₂ (альтернативная гипотеза заключается в том, что генеральное среднее одной совокупности больше генерального среднего другой совокупности).
• H₁: µ_1<µ₂ (альтернативная гипотеза заключается в том, что генеральное среднее одной совокупности меньше генерального среднего другой совокупности).

Давайте рассмотрим, как формулируются статистические гипотезы на конкретном примере.

Пример 1. В эксперименте участвуют две группы спортсменов. Эти группы перед экспериментом не имеют различий. Это означает, что спортсмены, входящие в эти группы, приблизительно равны по антропометрическим и физическим качествам и одинаково подготовлены.

Одна из групп (контрольная) тренируется по традиционной методике, вторая (экспериментальная) – по экспериментальной методике. Насколько эффективна новая (экспериментальная) методика, можно оценить по различию результатов, показанных спортсменами этих групп после определённого тренировочного цикла.

Для того, чтобы оценить эффективность экспериментальной методики выдвигаются статистические гипотезы. В данном случае нулевая гипотеза  – это гипотеза об отсутствии различий в результатах, показанных спортсменами после эксперимента. Она записывается так: H₀: µ_эг=µ_кг ,  где: µ_эг — среднее арифметическое генеральной совокупности спортсменов, которые тренируются по экспериментальной методике; µ_кг — среднее арифметическое генеральной совокупности спортсменов, которые тренируются по контрольной методике.

Альтернативная гипотеза – это гипотеза о значимости различий результатов, показанных спортсменами после эксперимента. Она может состоять в том, что средние арифметические двух генеральных совокупностей не равны: H₁: µ_1≠µ₂  (такая гипотеза принимается в том случае, если мы не знаем, результаты спортсменов какой группы окажутся лучше: контрольной или экспериментальной). Или, можно принять альтернативную гипотезу, которая состоит в том, что результаты  спортсменов экспериментальной группы лучше, чем результаты спортсменов контрольной группы. Тогда эту гипотезу запишем следующим образом: H₁:µ_эг>µ_кг.

Ошибки при проверке гипотез

Ошибки, допускаемые при проверке статистических гипотез, делятся на два типа:

• ошибки первого рода;
• ошибки второго рода.

Ошибка первого рода – отклонение гипотезы Н₀, когда она верна. Вероятность ошибки первого рода обозначается α и называется уровнем значимости критерия (рис.1).

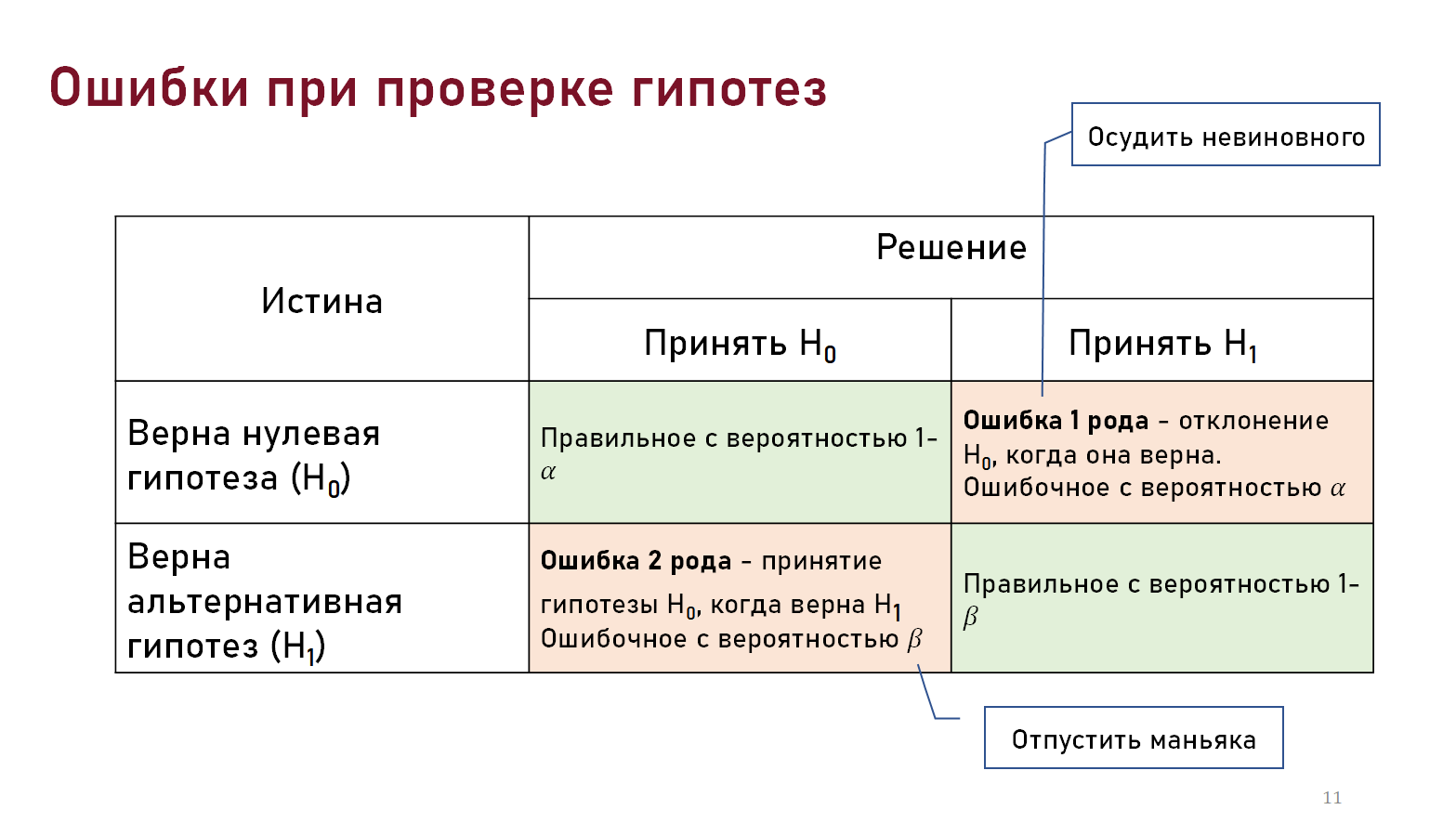
Ошибка второго рода – принятие гипотезы Н₀, когда верна альтернативная гипотеза. Вероятность ошибки второго рода обозначается β. Ее величина зависит от альтернативной гипотезы H₁. Величина 1- β называется мощностью критерия.

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
3. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
4. Лакин Г.Ф. Биометрия.- М.: Высшая школа, 1980.- 293 с.
5. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
6. Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.

С уважением, А.В. Самсонова