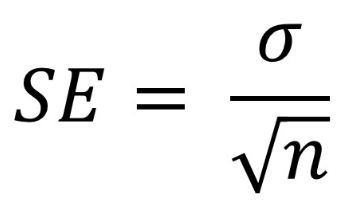
Стандартная ошибка среднего арифметического (теория и практика)
Среднее арифметическое, вычисленное на основе данных, полученных на основе выборки (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее арифметическое (чтобы рассчитать генеральное среднее арифметическое нужно измерить все объекты генеральной совокупности, а их достаточно много).
Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет принимать различные значения.
Проиллюстрируем это следующим примером.
Имеются 50 результатов, показанных юношами 15-16 лет в беге на 100 м (таблица 1). Будем условно считать эти результаты генеральной совокупностью. Среднее арифметическое для этой совокупности равно 15, 382 с
Таблица 1 Результаты в беге, показанные юношами 15-16 лет в беге на 100 м (n=50)
| 16,2 | 15,4 | 15,5 | 14,7 | 14,3 | 12,8 | 16,6 | 16,9 | 15,8 | 15,0 |
| 15,4 | 16,8 | 14,5 | 16,0 | 14,8 | 14,6 | 16,1 | 15,6 | 15,8 | 16,1 |
| 15,3 | 17,8 | 16,0 | 15,6 | 13,7 | 15,0 | 16,1 | 15,6 | 16,2 | 15,0 |
| 15,3 | 16,2 | 15,5 | 15,5 | 14,8 | 13,6 | 14,2 | 16,4 | 16,2 | 15,2 |
| 15,3 | 15,9 | 15,8 | 15,0 | 14,2 | 14,2 | 15,8 | 16,4 | 14,2 | 14,2 |
Теперь сформируем пять пять выборок по 10 результатов (результаты первой строки составляют первую выборку, второй — вторую и т.д), то есть объем каждой выборки будет равен n=10 и сосчитаем среднее арифметическое каждой выборки.
Получаем следующие результаты:
Среднее арифметическое первой выборки равно m1 = 15, 32 с
Среднее арифметическое второй выборки равно m2 = 15, 57 с
Среднее арифметическое третьей выборки равно m3 = 15, 63 с
Среднее арифметическое четвертой выборки равно m4 = 15, 29 с
Среднее арифметическое пятой выборки равно m5 = 15, 1 с
Как видим, полученные выборочные средние арифметические действительно не совпадают с средним арифметическим, рассчитанным на совокупности, состоящим из 50 результатов. Одни из них меньше генерального среднего (первая, четвертая и пятая выборки), а другие — больше (вторая и третья выборки). И это не ошибки измерений, а статистические ошибки, связанные с отбором результатов спортсменов в каждую выборку. Поэтому эти ошибки называют ошибками репрезентативности. Теперь дадим определение стандартной ошибки среднего арифметического.
Определение
Стандартная ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если вместо генерального среднего арифметического рассчитывать среднее арифметическое выборки.
Вычисление стандартной ошибки среднего арифметического
Стандартная ошибка среднего арифметического, обозначается буквой m или ![]()
В англоязычной научной литературе стандартная ошибка среднего арифметического обозначается SE (Standard Error).
Стандартная ошибка среднего арифметического рассчитывается по формуле:
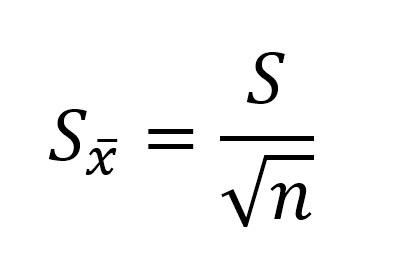
где: S — стандартное отклонение, n – объем выборки;
Например, если стандартное отклонение равно S=5 см, а объем выборки составляет n=36, то стандартная ошибка среднего арифметического равна:
m=5/6 = 0,833.
Из формулы следует, что чем больше объем выборки и чем меньше значение стандартного отклонения, тем меньше значение стандартной ошибки среднего арифметического. И наоборот, если объем выборки небольшой, а вариативность выборки большая, то значение стандартной ошибки среднего арифметического будет большим.
Буланов Н.М. с соавт. (2021) считают, что очень большие значения стандартной ошибки среднего арифметического могут свидетельствовать о наличии смещения, что мешает сделать корректные выводы.
Литература
- Буланов Н.М., Суворов А.Ю., Блюсс О.Б., Мунблит Д.Б., Бутнару Д.В., Надинская М.Ю., Заикин А.А. Основные принципы применения описательной статистики в медицинских исследованиях // Сеченовский
вестник. 2021; 12(3): 4–16. https://doi.org/10.47093/2218-7332.2021.12.3.4-16 - Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
- Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.
С уважением, А.В. Самсонова
- Учебные пособия по статистике
- Видеоуроки по Statgraphics
- Введение в математическую статистику
- Генеральная совокупность и выборка
- Статистические шкалы
- Эмпирические распределения
- Числовые характеристики выборки
- Стандартная ошибка среднего арифметического
- Представление результатов исследования
- Точечное и интервальное оценивание числовых характеристик
- Элементы теории вероятностей
- Нормальный закон распределения (закон нормального распределения)
- Статистические гипотезы
- Критерии проверки статистических гипотез
- Критерии согласия
- Обоснование выбора критерия значимости
- Параметрические критерии
- Статистические операции в номинальной шкале
- Представление данных статистического анализа
- Корреляционный анализ
- Представление данных корреляционного анализа
- Регрессионный анализ
- Представление результатов регрессионного анализа