Регрессионный анализ

Регрессионный анализ (теория и практика)

Определение

Регрессионный анализ — раздел математической статистики, устанавливающий формы зависимости между случайной величиной Y и значениями одной или нескольких переменных величин, причем значения последних считаются точно заданными.

Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии).

Использование в области физической культуры и спорта

В области физической культуры и спорта (ФКиС) регрессионный анализ применяется для:

1. Прогноза результатов (рекордов) на основе математической модели.
2. Вычисление значения признака, который напрямую измерить достаточно трудно.
3. Определение результата, который должен показать спортсмен в соревновательном упражнении, на основе измерения результата в тесте.
4. Выявление недостатков в развитии физических качеств.

1. Прогноз рекордов на основе математической модели

В области ФКиС регрессионный анализ часто используется для прогноза результатов (рекордов) на основе математической модели. Однако, когда прогноз распространяется за пределы исследуемых данных интерпретировать результаты необходимо с особой осторожностью.

Например, Л.Е.Садовский и А.Л.Садовский в книге «Математика и спорт» в 1985 году на основе анализа мировых рекордов по прыжкам с шестом у мужчин предложили линейную регрессионную модель:

Y= — 79,2049+0,0429466X,

где: Y — результат в прыжках в высоту с шестом у мужчин, м; X — год установления рекорда.

Согласно этой модели мировой рекорд в 2005 году должен был быть равен:

Y= — 79,2049+0,0429466X = — 79,2049+0,0429466*2005=6,90 м

Однако даже в 2024 году рекорд мира в прыжках с шестом у мужчин равен только 6,26 м. Он установлен Armand Duplantis 25.08.2024 г.

Это означает, что предложенная Л.Е.Садовским и А.Л.Садовским математическая модель неверна. Она хорошо описывала результаты 80-х годов ХХ века, но выход за пределы исследуемых данных дал неверные результаты.

2. Вычисление значения признака, который напрямую измерить достаточно трудно

Второй областью применения регрессионного анализа является вычисление значений признака, который напрямую измерить достаточно трудно. Например,  уравнение регрессии используется для вычисления МПК по результатам теста Купера.

Тест Купера. Тест должен выполняться на дорожке стадиона. После старта участники тестирования пытаются в течение 12 мин. преодолеть как можно большую дистанцию. Регистрируется расстояние (с точностью до 1 м), которое исследуемый преодолел за 12 минут. Уравнение регрессии имеет следующий вид:

МПК=0,0268 х (преодоленная дистанция) – 11,3,

где: МПК, мл/кг мин., а преодолеваемая дистанция – мили.

3. Определение результата, который должен показать спортсмен в соревновательном упражнении, на основе измерения результата в тесте

Третьей областью применения регрессионного анализа является определение результата, который должен показать спортсмен в соревновательном упражнении, на основе измерения результата в тесте. Дело в том, что не всегда перед соревнованиями можно протестировать спортсмена в соревновательном упражнении, чтобы определить его вероятный результат. Например, перед соревнованиями в марафонском беге спортсмен не может бежать марафонскую дистанцию, потому что это приведет к ухудшению результатов, показанных на соревнованиях. Поэтому тренеру приходится судить о готовности спортсмена к соревнованиям на основе различных показателей, в том числе и тестов.

4. Выявление недостатков в развитии физических качеств

Зачастую у тренера занимается группа спортсменов, которые тренируются в одном виде спорта. Например, в спринтерском беге на 100 м. Известно, что результат в беге на 100 м складывается из нескольких показателей: умения спортсмена выполнять стартовый разгон, максимальной скорости бега по дистанции и скоростной выносливости, то есть способности максимально долго удерживать максимальную скорость. Тестирование группы спортсменов в беге на 30 м и на 100 м позволила получить регрессионную модель:

beg100 = -1,2 + 3*beg30, где: beg 100 – результат в беге на 100 м, с; beg 30 – результат в беге на 30 м, с (рис. 1).

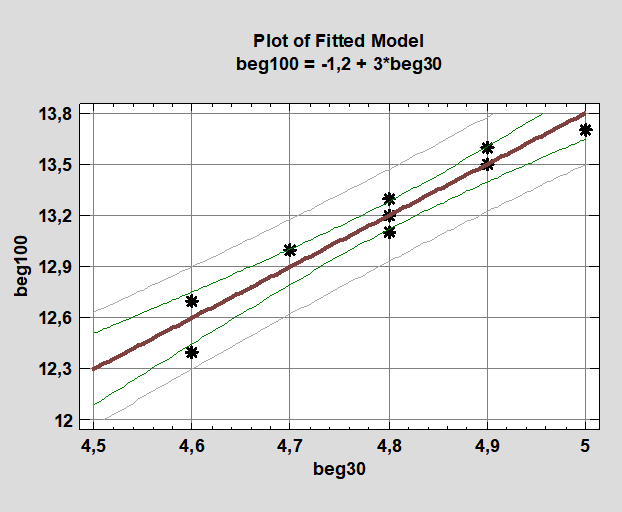
Из графика следует, что в беге на 30 м лучший результат — 4,6 с показали два спортсмена. Однако один из них показал в беге на 100 м результат 12,4, что лучше результата по группе, а второй спортсмен показал результат 12,7, что хуже результата по группе. Следовательно, второй спортсмен отстает в развитии скоростной выносливости. Показанный им результат в беге на 30 м говорит о хороших скоростных качествах, однако удержать максимальную скорость до финиша он не в состоянии.

Регрессионная модель

Самый важный этап регрессионного анализа – выбор подходящей регрессионной модели.

Регрессионная модель – это математическое выражение, связывающее значения зависимой случайной величины Y и значения независимой случайной величины Х.

Существуют различные регрессионные модели:

• простой регрессии;
• полиномиальной регресии
• множественной регрессии.

Модели простой регрессии

Модели простой регрессии построены на элементарных математических функциях:

Y=а+bX — уравнение прямой

Y= exp(a+bX) — экспонента

Y= aX^b — уравнение степенной функции

Модель полиномиальной регрессии

Модель полиномиальной регрессии имеет следующий вид:

Y=b₀+b₁X+b₂X²+…+b_nXⁿ

Модель множественной регрессии

Модель множественной регрессии выражается формулой:

Y= b₀+b₁X₁+b₂X₂+…b_nX_n

Последовательность регрессионного анализа

Приступая к регрессионному анализу, необходимо оценить:

1. значимость (достоверность) коэффициентов модели.
2. адекватность модели.

Проверку значимости коэффициентов регрессии осуществляем по критерию Стьюдента. Если p-value < 0,05 – коэффициенты регрессии значимы (достоверны). В статистических пакетах значение p-value выводится рядом с коэффициентами уравнения регрессии.

Адекватность регрессионной модели

Для оценки адекватности модели существует несколько критериев:

• Критерий Фишера
• Коэффициент детерминации (R² );
• Стандартная ошибка предсказания;
• График «наблюдение-предсказание».

Коэффициент детерминации

R² (R-squared) — коэффициент детерминации. R²=74,5% показывает, что на 74,5% расчетные параметры модели (то есть сама модель), объясняют зависимость и изменения изучаемого параметра Y от исследуемых факторов -X. Или другими словами коэффициент детерминации показывает, какая доля вариации объясняемой переменной учтена в модели и обусловлена влиянием на нее факторов, включенных в модель.

Чем ближе к коэффициент детерминации к 100% тем выше адекватность модели. Считается неплохо, когда R² больше чем 80%. Если коэффициент детерминации меньше 50%, то адекватность модели можно смело ставить под большой вопрос.

Стандартная ошибка предсказания

Мерой качества приближенного описания реальной зависимости между Y и X является стандартная ошибка предсказания (Standard Error of Est.). Чем ближе наблюдаемые значения к предсказываемым, тем меньше стандартная ошибка предсказания.

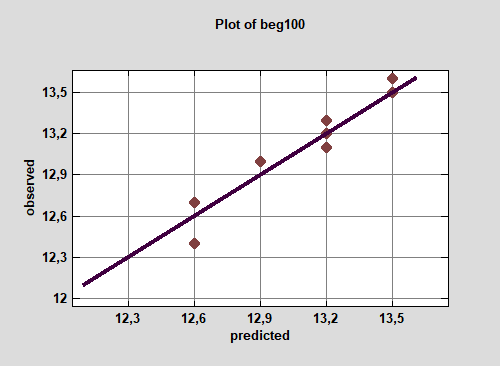
График «наблюдение-предсказание» или по-английски «observed-predicted» — график, в котором координаты точек по оси Х соответствуют значениям переменной, которые рассчитываются на основе уравнения регрессии, а координаты по оси Y — наблюдаемым значения признака. Если подобранная модель характеризуется высокой адекватностью — все точки должны лежать на линии, которая является биссектрисой угла (рис. 2).

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова. – М.: Физкультура и спорт, 1990. 176 с.