Представление результатов регрессионного анализа

ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РЕГРЕССИОННОГО АНАЛИЗА (в магистерской или кандидатской диссертациях)

Очень важно не только правильно выполнить регрессионный анализ, но и представить результаты расчетов в научной публикации.

В качестве примера приведем текст, который должен быть помещен в разделы магистерской диссертации: методы исследования (глава 2) и результаты исследований (глава 3).

Задание: установить зависимость между результатами в прыжке в высоту с места и результатами в толчке у тяжелоатлетов 1 разряда (весовая категория 60 кг), таблица 1.

Таблица 1 — Результаты в прыжке в высоту с места и в толчке у тяжелоатлетов 1 разряда (вес до 60 кг), n=12

№	Результат прыжка в высоту с места, см	Результат в толчке, кг
1	57	107,5
2	60	110
3	58	110
4	61	115
5	63	115
6	58	107,5
7	55	107,5
8	64	120
9	65	122,5
10	64	112,5
11	66	120
12	61	110

Более подробно о методах статистической обработки данных рассказано в книгах:

В результате обработки данных в пакете Statgraphics были получены следующие результаты:

Simple Regression — push vs. jump

Dependent variable: push

Independent variable: jump

Reciprocal-Y squared-X: Y = 1/(a + b*X^2)

Coefficients

	Least Squares	Standard	T
Parameter	Estimate	Error	Statistic	P-Value
Intercept	0,0120651	0,000522695	23,0824	0,0000
Slope	-8,59439E-7	1,39231E-7	-6,17275	0,0001

Analysis of Variance

Source	Sum of Squares	Df	Mean Square	F-Ratio	P-Value
Model	0,00000145898	1	0,00000145898	38,10	0,0001
Residual	3,82906E-7	10	3,82906E-8
Total (Corr.)	0,00000184189	11

Correlation Coefficient = -0,890007

R-squared = 79,2112 percent

R-squared (adjusted for d.f.) = 77,1324 percent

Standard Error of Est. = 0,00019568

Mean absolute error = 0,000149912

Durbin-Watson statistic = 1,91663 (P=0,3863)

Lag 1 residual autocorrelation = -0,0248744

Коэффициент детерминации (R-squered) равен 79,2112%. Коэффициенты уравнения регрессии следующие: а=0,0120651; -8,59439E-7. Стандартная ошибка предсказания равна 0,00019568.

Текст в магистерскую или кандидатскую диссертацию

Регрессионный анализ использовался с целью установления зависимости между результатом в прыжке в высоту с места и результатом в толчке у тяжелоатлетов 1 разряда (весовая категория до 60 кг).

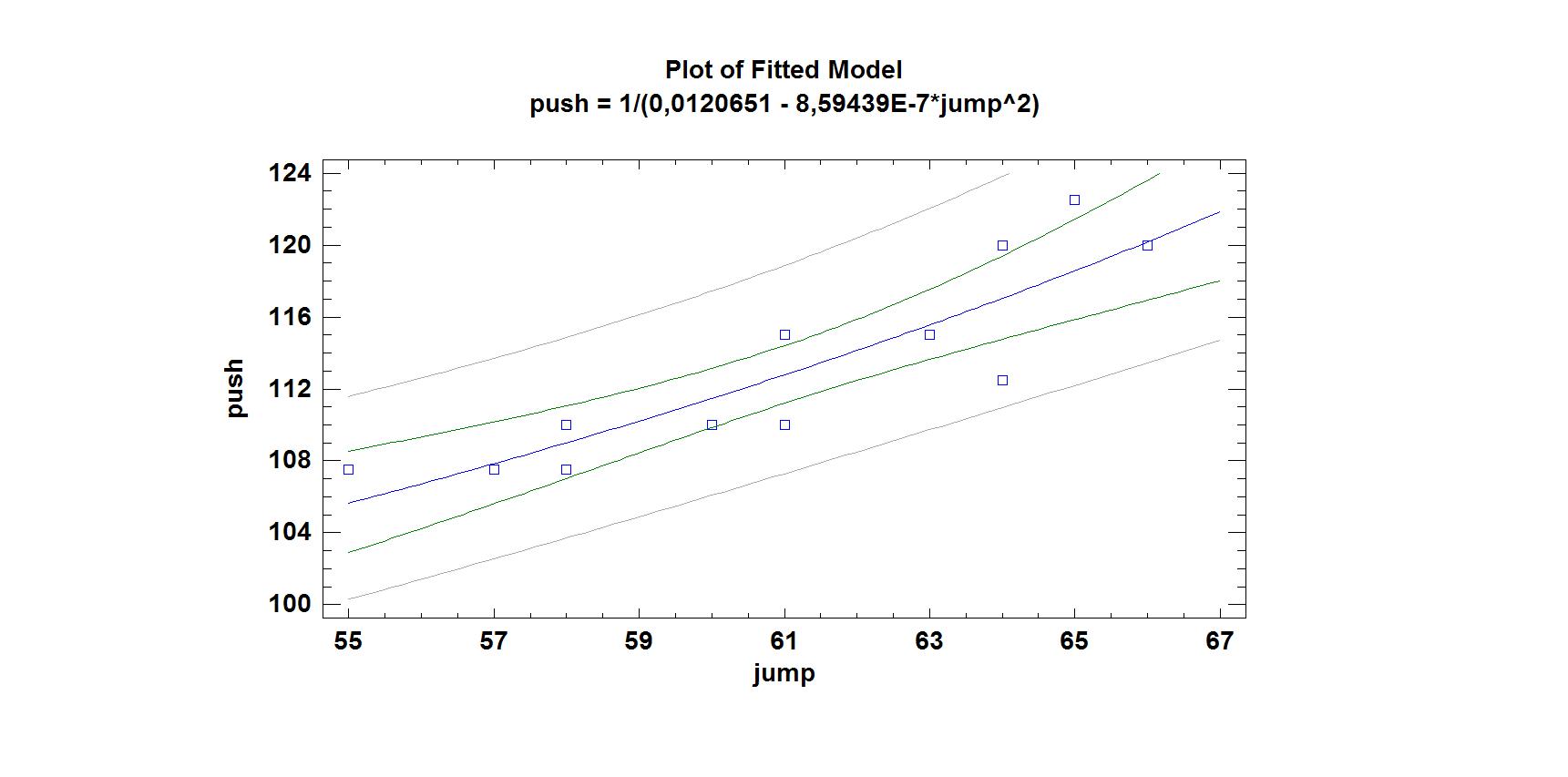
Адекватность подобранной модели оценивалась на основе коэффициента детерминации. Наибольший коэффициент детерминации оказался у модели, уравнение регрессии которой имеет вид: Y=1/(a+bX²). Он равен 79,2%. Значимость коэффициентов уравнения регрессии оценивалась по t-критерию Стьюдента, так как P-value <0,001, коэффициенты регрессии значимы. Стандартная ошибка предсказания равна 0,00019568. Полученное уравнение регрессии имеет вид:

Y=1/(0,0120651 – 8,59439 10^-7 x),

где: x – результат в прыжке; Y – результат в толчке.

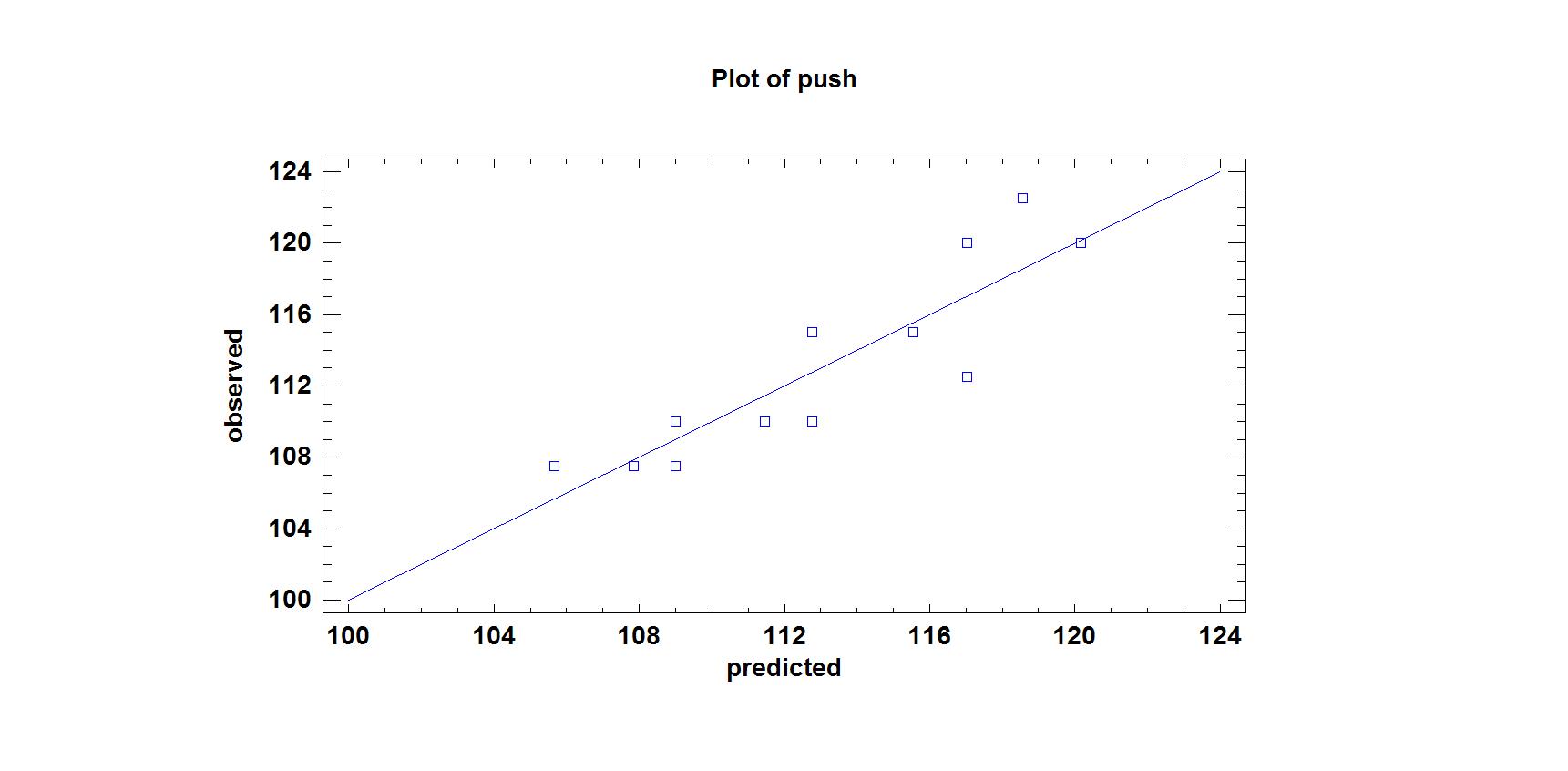
На рис.1 представлен график подобранной модели с доверительным интервалом и интервалом возможных прогнозируемых значений Y. На рис. 2 представлен график предсказанных и наблюдаемых значений.

График регрессионной модели — Рис.1. График подобранной регрессионной модели

График Предсказание (ось Х) - наблюдение (ось Y) — Рис.2. График Предсказание (ось Х) — наблюдение (ось Y)

Литература

Дюк В. Обработка данных на ПК в примерах.– СПб: Питер, 1997.– 240 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ. / /Под ред. В.С. Иванова. М.: Физкультура и спорт, 1990.– 176 с.

С уважением, А.В. Самсонова