Представление данных корреляционного анализа

Представление данных корреляционного анализа в научных исследованиях

Традиционно данные корреляционного анализа представляются в виде корреляционной матрицы (табл. 1) или корреляционного поля.

Корреляционная матрица (матрица корреляций) – это квадратная таблица, заголовками строк и столбцов которой являются обрабатываемые переменные, а на пересечении строк и столбцов выводятся коэффициенты корреляции для соответствующей пары признаков.

Например, в табл. 1 для пары переменных x1x2, коэффициент корреляции равен 0,8516 (он выделен красным цветом, а переменные — жирным шрифтом).

Корреляционная матрица обладает следующими свойствами:

На главной диагонали находятся коэффициенты корреляции, равные единице.
Матрица симметрична относительно главной диагонали.

Таблица 1 — Корреляционная матрица

	x1	x2	x3	x4
x1	1	0,8516	0,4410	0,7923
x2	0,8516	1	0,4428	0,6581
x3	0,4410	0,4428	1	0,2820
x4	0,7923	0,6581	0,2820	1

После выполнения расчетов в пакете STATGRAPHICS корреляционная матрица выглядит следующим образом (рис.1), на главной диагонали цифра «1» не стоит. Однако в пакете STATGRAPHICS выводится дополнительная информация:

На пересечении пары переменных в ячейке матрицы записываются три значения:

Верхнее значение: коэффициент корреляции (r);
Среднее (в скобках) – объем выборки (n)
Нижнее – значение p-value (это позволяет сразу определить достоверность вычисленного коэффициента корреляции).

По значению p-value можно сразу определить достоверность вычисленного коэффициента корреляции. Правило такое: если p-value <0,05, то коэффициент корреляции достоверен.

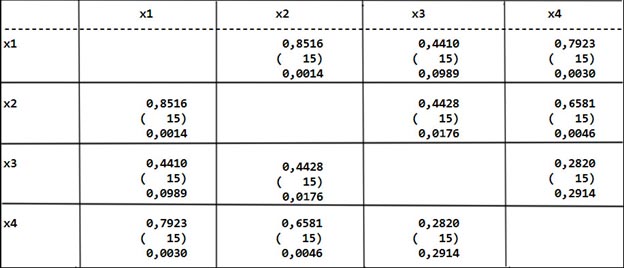
Рис.1. Корреляционная матрица, полученная после обработки результатов в пакете Statgraphics

В корреляционной матрице, представленной на рис. 1 достоверны все коэффициента корреляции, кроме коэффициента корреляции, равного 0,2820 (для пары x3x4), потому что p-value равно 0,2914. Это число больше 0,05. Поэтому коэффициент корреляции недостоверен.

Более подробно о методах статистической обработки данных рассказано в книгах:

Для представления данных корреляционного анализа используется несколько способов.

Первый способ

Значимость коэффициентов корреляции определяется на основе приведенного в заголовке таблицы критического значения коэффициента корреляции (r_крит) при определенном уровне значимости α. Также в заголовке таблицы приведен объем выборки (n). Для читающего таблицу с таким представлением информации ясно, что все коэффициенты корреляции, значения которых больше критического являются значимыми.

Таблица 2 — Значения коэффициентов корреляции между результатами в скоростно-силовых тестах и результатом в толкании ядра с разгоном n=32, спортивный результат группы варьировал от 12,00 м до 20,50. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r_0,05= 0,349 (Я.Е.Ланка, Ан.А.Шалманов, 1982).

	Упражнение	1	2	3	4	5	6
1	Толкание ядра с разгона	1	0,97	0,84	0,83	0,73	0,73
2	Толкание ядра с места		1	0,84	0,82	0,74	0,76
3	Бросок ядра назад			1	0,85	0,71	0,66
4	Бросок ядра вперед				1	0,66	0,62
5	Приседание со штангой					1	0,58
6	Жим штанги лежа						1

Второй способ

Второй способ представления информации характеризуется тем, что в корреляционной матрице оставляются только значимые коэффициенты корреляции. Если коэффициенты корреляции недостоверны, в ячейке ставится прочерк (табл.3). В примечании внизу таблицы указывается, что прочерк означает недостоверность коэффициента корреляции.

Таблица 3 — Корреляционная матрица результатов мальчиков-пловцов 13 лет, (n= 13)

№	Тест	1	2	3	4	5
1	Темп, гр/мин	1	—	—	—	—
2	Время проплывания 25 м, с		1	0,911	0,679	0,859
3	Время проплывания 50 м, с			1	0,861	0,969
4	Время проплывания 100 м, с				1	0,865
5	Время проплывания 200 м, с					1

Примечание: «-» — коэффициент корреляции недостоверен, р >0,05

Третий способ

Третий способ представления данных корреляционного анализа наиболее распространен как в Российских научных публикациях, так и в зарубежных. В заголовке таблицы указывается, что это корреляционная матрица, указывается также объем выборки (n).

Значимость коэффициента корреляции обозначается знаком звездочка (*), который ставится над коэффициентом корреляции в правом верхнем углу ячейки.

Правило следующее: одна звездочка (*) ставится при p<0,05; две звездочки (**) ставятся, при p<0,01; три звездочки (***) ставятся при р<0,001. Если у значения коэффициента корреляции нет знака звездочки (*) — это означает, что он недостоверен. В табл.4. показан вариант представления данных третьим способом. Необходимо в примечании под таблицей указать, что означают эти звездочки.

Таблица 4 — Корреляционная матрица результатов мальчиков-пловцов 13 лет, (n= 13)

№	Тест	1	2	3	4	5
1	Темп, гр/мин	1	0,135	0,167	0,371	0,105
2	Время проплывания 25 м, с		1	0,911^***	0,679^*	0,859^***
3	Время проплывания 50 м, с			1	0,861^***	0,969^***
4	Время проплывания 100 м, с				1	0,865^***
5	Время проплывания 200 м, с					1

Примечание: * – коэффициент корреляции достоверен, р<0,05; *** – коэффициент корреляции достоверен, р<0,001.

Иногда в исследованиях представление результатов корреляционного анализа выглядит следующим образом (рис. 2)

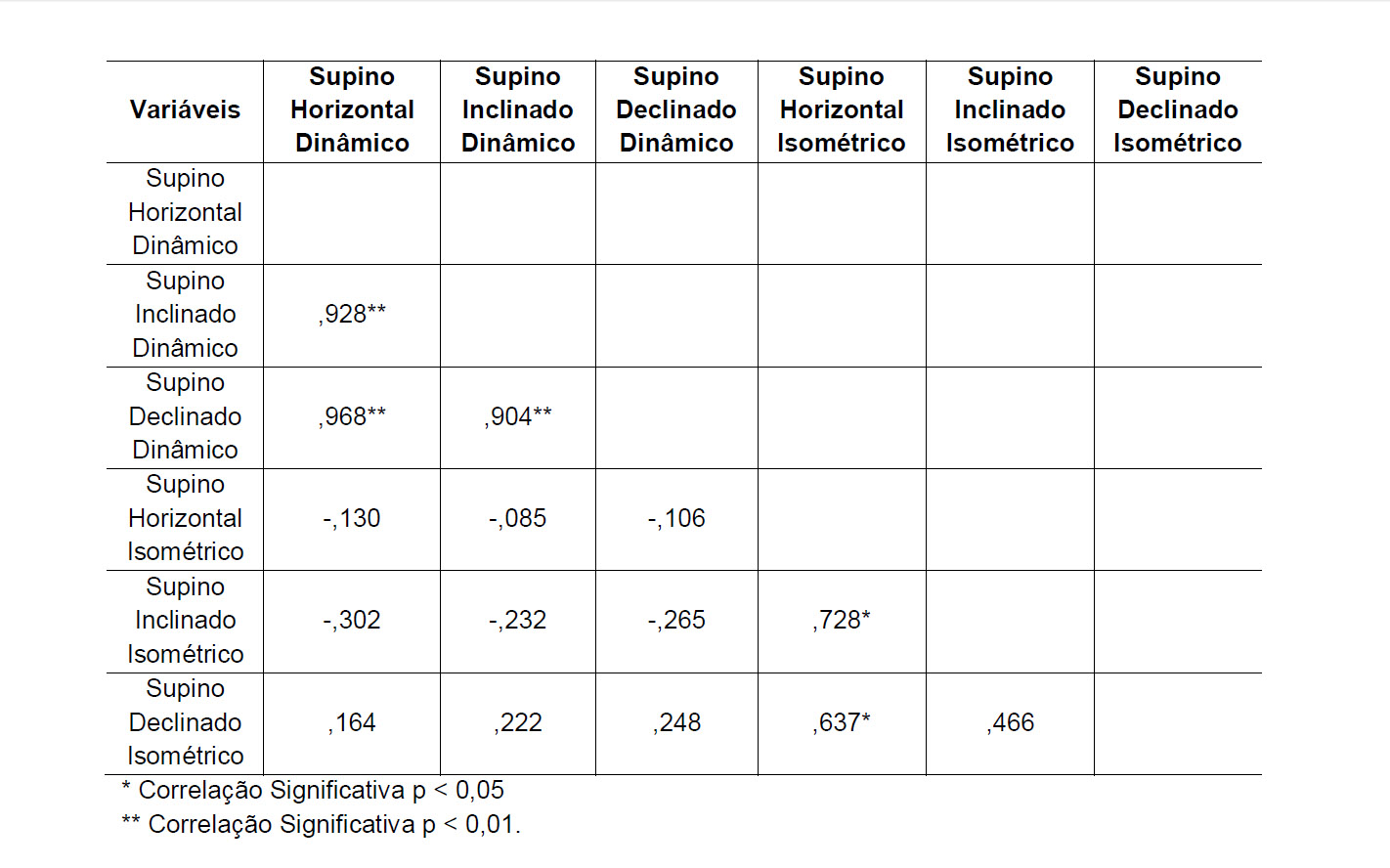
Рис.2. — Корреляционная матрица результатов различных вариантов жима штанги лежа (Penido L.N. et al., 2012)

В этом случае авторы разместили коэффициенты корреляции слева-внизу, опустили нули в записи коэффициентов корреляции и не проставили цифру 1 на главной диагонали. Однако внизу под таблицей указали, что означают звездочки. Все это допускается при записи корреляционной матрицы.

Литература

Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.