Параметрические критерии

Параметрические критерии проверки статистических гипотез

При проведении исследования часто формируются две группы; например, контрольная и экспериментальная, мужчин и женщин и т.д. В этом случае говорят о двух независимых выборках.

Правила проведения эксперимента требуют, чтобы перед его началом результаты участников контрольной группы незначительно отличались от результатов экспериментальной группы. В то же время после проведения эксперимента многие исследователи ожидают получить больший  эффект в группе, применяющей экспериментальную методику.

Следует, однако, учесть, что можно проверять различие характеристик положения (например, средних арифметических или медиан), а можно оценивать различие характеристик вариативности (дисперсий). На этот нюанс многие исследователи не обращают внимание, однако, иногда результат воздействия выражается не в изменении средних значений, а в изменении вариативности результатов.

Определение

Параметрическими критериями называются такие критерии, которые включают в формулу расчёта параметры распределения, например, параметрами нормального распределения являются: средние арифметические и дисперсии.

К параметрическим критериям, основанным на нормальном распределении, относятся:

• F-критерий Фишера;
• t-критерий Стьюдента (независимые выборки);
• t-критерий Стьюдента (связанные выборки).

Условия использования параметрических критериев

Первое условие

Первым условием использования параметрических критериев, основанных на нормальном распределении генеральной совокупности, является нормальное распределение признака.

Поэтому прежде использовать параметрический критерий, в формулу которого включены параметры нормального распределения, необходимо быть точно уверенным, что распределение исследуемого признака соответствует нормальному закону. С этой целью нужно использовать критерии согласия. Если распределение признака не соответствует нормальному закону, для проверки статистических гипотез нужно использовать непараметрические критерии.

Второе условие

Вторым условием является непрерывное распределение признака (случайной величины). То есть, использовать параметрические критерии можно только если распределение признака непрерывно.

Поясним это условие. Известно, что распределение случайных величин может быть дискретным или непрерывным.

Случайная величина называется дискретной если множество ее значений конечно или счетно (может быть занумеровано натуральными числами, т.е.1,2,3 и т.д.). Например, количество попаданий в кольцо из 10 штрафных бросков (конечное) или количество подтягиваний на турнике (счетное).

Случайная величина называется непрерывной, если она может принимать любые значения из некоторого промежутка. Число значений непрерывной случайной величины бесконечно. Например, признак рост является непрерывной случайной величиной.

Третье условие

Третьим условием применения параметрических критериев является статистическая шкала, в которой представлены экспериментальные данные. Существуют четыре статистических шкалы: номинальная, порядковая, интервальная и шкала отношений.

Параметрические критерии можно применять к данным, представленными в интервальной шкале и шкале отношений, то есть экспериментальные результаты должны измеряться  в кг, м, с (система СИ) и т.д. Если результаты эксперимента представлены в баллах (это порядковая статистическая шкала) использовать параметрические критерии нельзя. В этом случае необходимо применять непараметрические критерии.

Вывод

Чтобы применять параметрические критерии для проверки статистических гипотез, необходимо, чтобы были выполнены следующие условия:

• нормальное распределение признака;
• непрерывное распределение признака;
• исследуемый признак измеряется с использованием интервальной шкалы или шкалы отношений.

Только в этом случае экспериментальные данные будут обработаны правильно.

Критерий F-Фишера (независимые выборки)

Следует отметить, про при использовании критерия Стьюдента, применяются разные формулы в зависимости от того, существуют ли достоверные различия в вариативности результатов. Поэтому перед применением критерия Стьюдента необходимо проверить гипотезу о равенстве дисперсий генеральных совокупностей, из которых взяты выборки. С этой целью применяется F-критерий, который разработан английским математиком Рональдом Фишером (рис.1).

Этот критерий применяется в том случае, если необходимо проверить гипотезу о том, что две независимые выборки получены из генеральных совокупностей с одинаковыми дисперсиями.

Порядок вычисления критерия Фишера

1.Выдвигаются нулевая (Н₀) и альтернативная (Н₁) гипотезы.

• Н₀: σ₁²= σ₂²
• Н₁: σ₁²≠σ₂²

где: σ₁² — дисперсия первой генеральной совокупности; σ₂² — дисперсия второй генеральной совокупности.

2.Выбирается уровень значимости α=0,05.

3.Вычисляем фактическое значение критерия Фишера по формуле: F_ф=S₁²/S₂²

4. Если F_ф ≥ F_крит (определяется на основе табличных значений) — гипотеза о равенстве дисперсий генеральных совокупностей отвергается на уровне значимости α.

Критерий t-Стьюдента (независимые выборки)

Критерий Стьюдента разработан английским математикам Уильямом Госсетом (рис.2) для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья У. Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

Критерий Стьюдента применяется в том случае, если необходимо проверить гипотезу о том, что две независимые выборки получены из генеральных совокупностей с одинаковыми средними арифметическими.

Порядок вычисления критерия Стьюдента (независимые выборки)

1.Выдвигается нулевая (Н₀) и альтернативная (Н₁) гипотезы:

Н₀ : µ₁= µ₂

Н₁ : µ₁≠ µ₂

где: µ₁ — среднее арифметическое первой генеральной совокупности; µ₂ — среднее арифметическое второй генеральной совокупности.

2.Выбирается уровень значимости α=0,05.

3.Вычисляется фактическое значение критерия Стьюдента для независимых выборок по одной из формул:

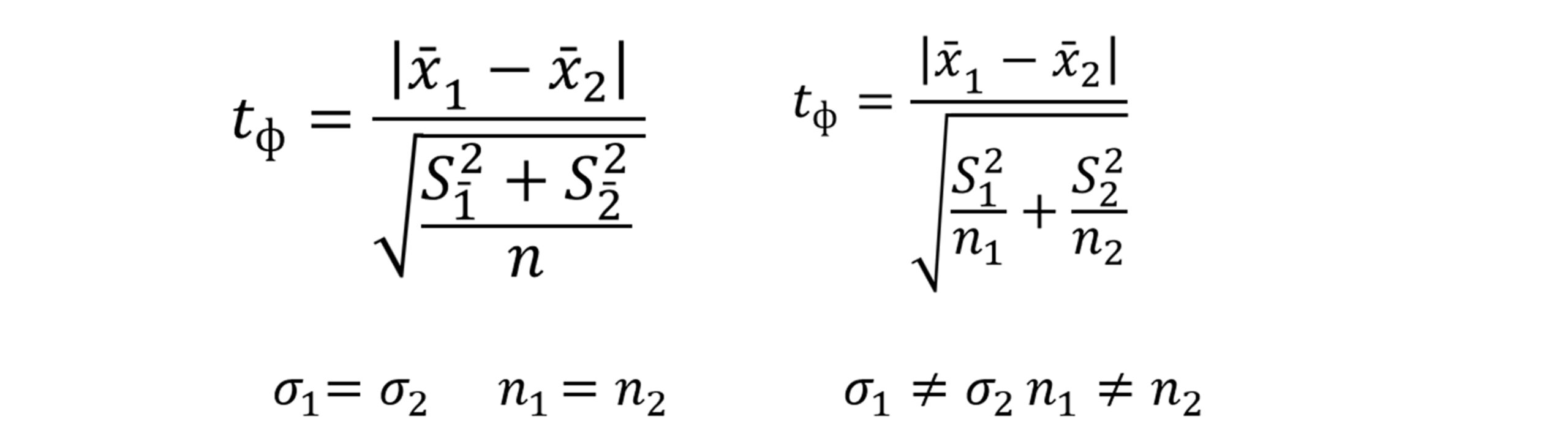
Формула слева используется при расчете фактического критерия Стьюдента при условии равенств стандартных отклонений (σ₁=σ₁) и объемов выборок (n₁=n₂), формула справа — при неравенстве стандартных отклонений (σ₁≠σ₁) и объемов выборок (n₁≠n₂).

Если t_ф ≥ t_крит (берется из таблицы) гипотеза о равенстве средних арифметических генеральных совокупностей отвергается на уровне значимости α.

Критерий t-Стьюдента (связанные выборки)

При использовании этого критерия гипотеза формулируется в отношении разностей пар наблюдений (d_i).

Порядок вычисления критерия Стьюдента (связанные выборки)

1.Выдвигается нулевая (Н₀) и альтернативная (Н₁) гипотезы.

Н₀: µ_d= 0

Н₁ : µ_d≠ 0,

где: µ_d — среднее арифметическое разности генеральной совокупности.

2.Выбирается уровень значимости α=0,05.

3.Вычисляется фактическое значение критерия Стьюдента для связанных выборок по формуле:

где: t_ф — фактическое значение критерия Стьюдента; d ̄ — среднее арифметическое разности; S_d — стандартное отклонение разности; n – объем выборки.

4.Если t_ф ≥ t_крит гипотеза о равенстве средних арифметических генеральных совокупностей отвергается на уровне значимости α.

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии.- М.: Прогресс, 1976.-495 с.
3. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
4. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
5. Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.

С уважением, А.В.Самсонова