Критерии согласия

Критерии согласия (теория и практика)

Определения

Критерием согласия называется критерий значимости, применяемый для проверки гипотезы о законе распределения генеральной совокупности, из которой взята выборка.

Чаще всего исследователя интересует, соответствует ли распределение экспериментальных данных нормальному закону. Поэтому примеры будут связаны с проверкой эмпирического распределения на нормальность. С этой целью наиболее часто используются следующие критерии:

Критерий Шапиро-Уилки
Критерий хи-квадрат
Критерий лямбда Колмогорова-Смирнова

Более подробно о методах статистической обработки данных рассказано в книгах:

Критерий Шапиро-Уилки

Разработан американским статистиком Самуэлем Сандфордом Шапиро и канадским статистиком Мартином Брадбари Уилком.

Статистики Самуэль Шапиро и Мартин Уилк разработчики критерия Шапиро-Уилки

Условия применения: выборка небольшого объема (n>8). Однако этот критерий хорошо работает и с выборками большого объема.

Статистические гипотезы:

Н₀ – распределение генеральной совокупности из которой получена выборка совокупности соответствует нормальному закону.

Н₁— распределение генеральной совокупности из которой получена выборка совокупности не соответствует нормальному закону.

Пример 1.

Имеем следующие значения: 11,8; 12; 12,1; 12,3; 12,6; 12,6; 12,8; 13; 13,2; 13,8. Алгоритм расчета представлен в табл.1.

Таблица 1 – Алгоритм расчета критерия Шапиро-Уилки

№	x	x	Δk	k	ank	ankΔk
1	2	3	4	5	6	7
1	11,8	13,8	2	1	0,5739	1,1478
2	12	13,2	1,2	2	0,3291	0,39492
3	12,1	13	0,9	3	0,2141	0,19269
4	12,3	12,8	0,5	4	0,1224	0,0612
5	12,6	12,6	0	5	0,0399	0
6	12,6	12,6
7	12,8	12,3		Сумма=b = 17966
8	13	12,1
9	13,2	12
10	13,8	11,8

Алгоритм расчета критерия Шапиро-Уилки

Формулируем гипотезу Н₀ о соответствии распределения генеральной совокупности, из которой получены данные нормальному закону. Назначаем уровень значимости α=0,05.
Получаем выборку экспериментальных данных (столбец 2 табл.1). В нашем случае n=10.
Рассчитываем значение выборочной дисперсии. Для приведенного примера дисперсия равна: S²=0, 37.
Ранжируем выборку в возрастающем и убывающем порядке (столбцы 2 и 3)
Считаем разности Δk (столбец 5) между значениями столбцов 2 и 3.
Из таблицы 6 Приложения (см. В.С.Иванов, 1990) находим значения коэффициентов ank (столбец 6)
Находим произведение ank*Δk
Вычисляем b=сумма ankΔk= 1,7966
Рассчитываем значение критерия W_ф по формуле:

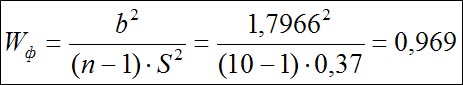
Формула расчета критерия Шапиро-Уилки

Из табл. 7 Приложения (см. В.С.Иванов, 1990) находим критическое значение критерия Шапиро-Уилки для α=0,05 W_крит= 0,842.
Вывод. Так как W_ф>W_крит, можно говорить, что экспериментальные данные соответствуют нормальному закону на уровне значимости 0,05.

Критерий хи-квадрат

Критерий хи-квадрат разработан английским статистиком Карлом Пирсоном в 1904 году.

Английский математик Карл Пирсон - разработчик критерия хи-квадрат

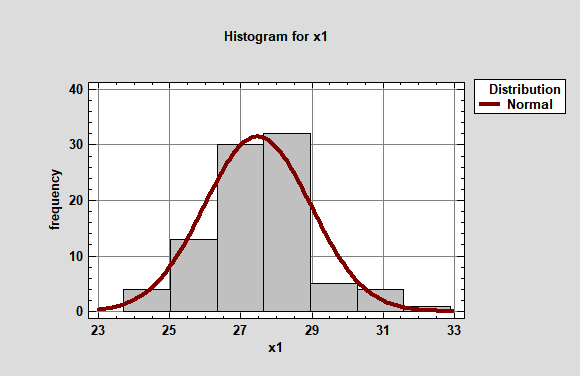
Основан на построении интервального вариационного ряда и сравнении эмпирических (n_эм) и теоретических (n_т) частот. На рис.2. представлена гистограмма, характеризующая эмпирическое распределение 50 результатов, показанных школьниками в беге. Высота каждого столбика характеризуется эмпирической частотой n_эм.Теоретическое нормальное распределение, показано вишневой линией.

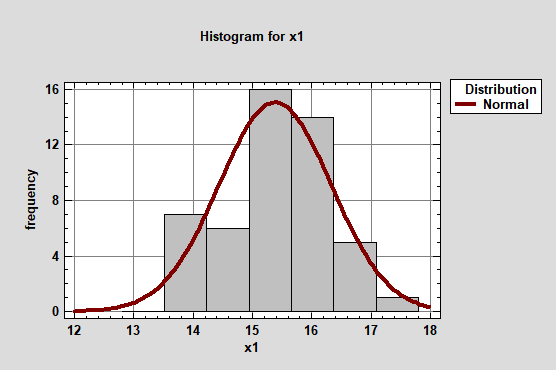
Рис.2. Гистограмма, характеризующая эмпирическое распределение и функция плотности вероятностей нормального распределения

Статистическая гипотеза заключается в том, что функция плотности распределения вероятностей генеральной совокупности, из которой взята выборка, соответствует теоретической модели нормального распределения. Значение фактического критерия хи-квадрат ( χ²_ф) вычисляется по формуле:

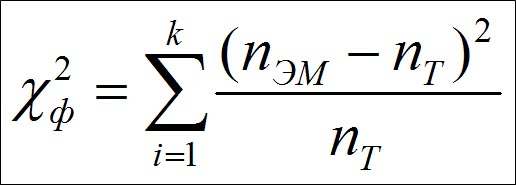
Формула расчета критерия хи-квадрат

Если фактическое значение критерия хи-квадрат больше или равно критическому значению критерия хи-квадрат, можно сделать вывод, что эмпирическое распределение не соответствует нормальному закону на уровне значимости α

Критерий Колмогорова-Смирнова (лямбда)

Разработан советскими математиками Андреем Николаевичем Колмогоровым и Николаем Васильевичем Смирновым.

Советские математики Андрей Николаевич Колмогоров и Николай Васильевич Смирнов - разработчики критерия лямбда Колмогорова-Смирнова

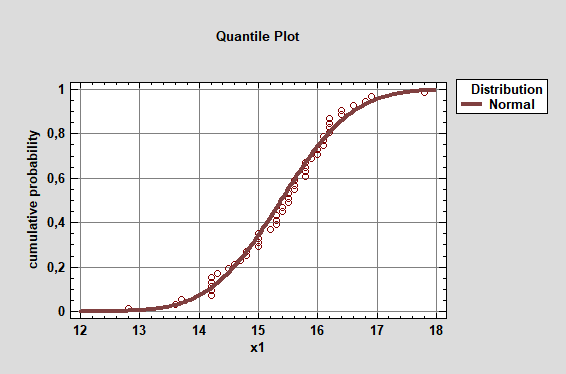
Статистическая гипотеза заключается в том, что функция распределения генеральной совокупности (рис. 3), из которой взята выборка, соответствует функции распределения нормального закона.

Красные точки - кумулята, построенная на основе экспериментальных данных, вишневая кривая - теоретическая функция распределения (нормальное распределение). — Рис.3. Красные точки — кумулята, построенная на основе экспериментальных данных, вишневая кривая — теоретическая функция распределения (нормальное распределение).

Значение критерия λ_ф вычисляется по формуле:

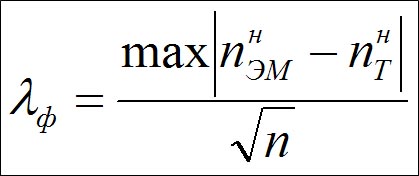
Формула расчета критерия лямбда (Колмогорова-Смирнова)

Вывод: если λ_ф> λ_крит– эмпирическое распределение не соответствует нормальному закону на уровне значимости α.

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

С уважением, А.В. Самсонова