Вариационные ряды (эмпирические распределения)
Обработка экспериментальных данных очень часто начинается с описательной статистики, которая включает методы построения эмпирических распределений (табличные и графические) и расчет числовых характеристик случайной величины (выборки).
В этом разделе мы разберем методы построения эмпирических распределений. С этой целью введем несколько определений.
Признак – свойство исследуемых объектов, которое позволяет их сравнивать и классифицировать.
На рис.1 представлены два объекта, которые мы пытаемся сравнить: яблоко и апельсин. Мы можем их сравнивать по разным признакам: цвету, сладости, наличию повреждений, весу.

Итак, вес — один из признаков по которому мы их можем сравнивать различные объекты и их классифицировать.
Варианта — отдельное числовое значение признака.
Например, масса апельсина (рис.1) равна 250 г, а яблока — 200 г. В данном случае — 250 г и 200 г — это две варианты. Значение одной варианты равно 250 г, а другой — 200 г.
Выборочные данные, полученные в ходе эксперимента, называются экспериментальными или эмпирическими данными. На основе этих данных можно построить эмпирическое распределение, то есть распределение элементов выборки по значениям изучаемого признака.
Построение эмпирического распределения (вариационного ряда)
Как же построить эмпирическое распределение признака? Построение эмпирического распределения (вариационного ряда) начинается с группировки. Она заключается в распределении вариант выборки либо по одинаковым значениям (в этому случае строится дискретный вариационный ряд), либо по интервалам (в этом случае строится интервальный вариационный ряд).
Построение дискретного вариационного ряда:
Пример 1. Двенадцать стрелков, выполняя упражнение лёжа, из 10 выстрелов показали следующие результаты (очки).
Таблица 1. Результаты (очки) в стрельбе лежа, показанные стрелками (n=12)
| 94 | 91 | 96 | 94 | 94 | 92 | 91 | 92 | 91 | 95 | 94 | 94 |
Переформируем этот ряд, записав полученные значения вариант (xi) в порядке возрастания (таблица 2). В столбце fн укажем абсолютную частоту признака, то есть число, показывающее, сколько раз варианта встречается (наблюдается) в выборке. Например, варианта 91 встречается в выборке три раза. Поэтому в первой строке таблицы 2 в столбце fн проставим число 3. Варианта 92 встречается в выборке два раза. Поэтому во второй строке проставим число 2. Варианта 94 встречается в нашей выборке пять раз. Поэтому в третьей строке таблицы 2 в столбце fн поставим число 5.
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта (электронная книга)
- Математическая статистика в спортивных исследованиях (электронная книга)
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
В таблице 3 кроме абсолютных частот проставим еще и относительные частоты.
Относительной частотой признака называется отношение абсолютной частоты к объему выборки.
В нашем примере объем выборки равен n=12. Поэтому если разделить 3 на 12 получим 0,250 (таблица 3 первая строка). Это и есть относительная частота, с которой варианта 91 встречается в выборке. Таким образом мы получили так называемые дискретные вариационные ряды с абсолютными (таблица 2), а также абсолютными и относительными частотами (таблица 3).
Таблица 2 Таблица 3
| № варианты | x | fн | № варианты | x | fн/n | |
| 1 | 91 | 3 | 1 | 91 | 0,250 | |
| 2 | 92 | 2 | 2 | 92 | 0,167 | |
| 3 | 94 | 5 | 3 | 94 | 0,417 | |
| 4 | 95 | 1 | 4 | 95 | 0,083 | |
| 5 | 96 | 1 | 5 | 96 | 0,083 | |
| Сумма (объем выборки) | 12 | Сумма относительных частот | 1 |
Построение интервального вариационного ряда
В случае непрерывных случайных величин (если измеряемые величины являются таковыми) и большого количества испытаний предпочтительнее составлять сгруппированный (интервальный) вариационный ряд. Он также представляется в виде таблицы, однако в столбце вариант указываются промежутки (диапазоны) значений измеренного признака. Проиллюстрируем это следующим примером.
Пример 2. Составить интервальный вариационный ряд на основе результатов бега на 100 м (с) юношей 15-16 лет:
| 16,2 | 15,4 | 15,5 | 14,7 | 14,3 | 12,8 | 16,6 | 16,9 | 15,8 | 15,0 |
| 15,4 | 16,8 | 14,5 | 16,0 | 14,8 | 14,6 | 16,1 | 15,6 | 15,8 | 16,1 |
| 15,3 | 17,8 | 16,0 | 15,6 | 13,7 | 15,0 | 16,1 | 15,6 | 16,2 | 15,0 |
| 15,3 | 16,2 | 15,5 | 15,5 | 14,8 | 13,6 | 14,2 | 16,4 | 16,2 | 15,2 |
| 15,3 | 15,9 | 15,8 | 15,0 | 14,2 | 14,2 | 15,8 | 16,4 | 14,2 | 14,2 |
Решение. Для лучшего понимания процесса группировки представим его в виде алгоритма.
Первый шаг состоит в нахождении числа интервалов группировки , с этой целью используем Таблицу 3, в которой представлена зависимость количества интервалов группировки от объёма выборки . В нашем примере объем выборки равен 50, то есть = 50, поэтому число интервалов группировки можно установить от 6 до 8. Давайте примем равным 7.
Таблица 3 – Зависимость количества интервалов группировки от объёма выборки
| Объём выборки, n | 25-40 | 40-60 | 60-100 | 100-200 | больше 200 |
| Количество интервалов, k | 5-6 | 6-8 | 7-10 | 8-12 | 10-15 |
Второй шаг состоит в определении размаха варьирования (R ) результатов. Для этого в выборке находят минимальное и максимальное значения признака. После чего вычисляют размах варьирования:
R = Xmax-Xmin.
В нашем случае Xmax равно 17,8 с, а Xmin равно 12,8 с. Тогда размах варьирования равен: R = 17,8 – 12,8 = 5 с.
Третий шаг состоит в нахождении ширины интервалов группировки по формуле h=R/k . Эту величину необходимо округлить до размерности измеряемого показателя, но всегда в большую сторону. В нашем случае, h=5/7=0,714. Округляем до 0,8 с, так как измерения производились с точностью до десятых долей секунды.
Составляем интервалы группировки таким образом, чтобы нижняя граница первого интервала группировки (Hlow) была меньше, чем минимальное значение Xmin, которое в нашем равно 12,8 с. Обычно это значение равно Xmin-h/2. В нашем примере за нижнюю границу принимается значение 12,8-0,8/2=12,4с. Тогда нижняя граница первого интервала будет равна 12,4 с, а верхняя – 12,4+0,8=13,2 с. Нижняя граница второго интервала группировки будет равна 13,2 с, а верхняя – 13,2+0,8 = 14,0 с, и так далее (Таблица 4).
Верхняя граница последнего интервала группировки (Hupp) будет равна 18,0 с. Затем подсчитываем, сколько результатов из Примера 2 попали в интервалы группировки, то есть подсчитываем абсолютные частоты. После этого считаем относительные частоты. С этой целью абсолютные частоты делим на объем выборки. Результаты заносим в табл.4.
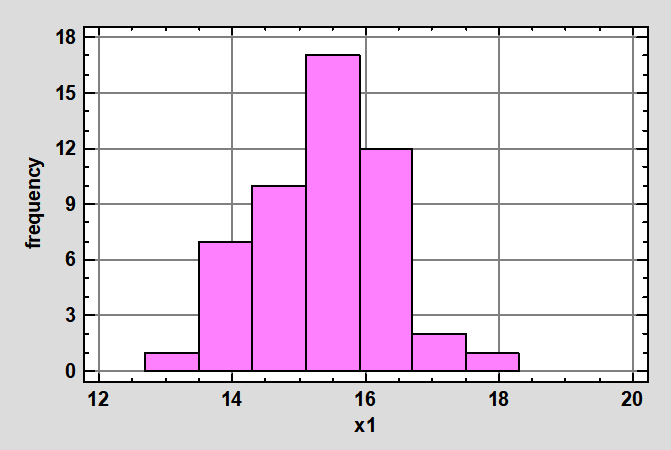
Таблица 4 – Интервальный вариационный ряд результатов бега на 100 м юношей
| № интервала | Интервалы группировки | fн | p |
| 1 | (12,4; 13,2] | 1 | 0,02 |
| 2 | (13,2; 14,0] | 2 | 0,04 |
| 3 | (14,0; 14,8] | 11 | 0,22 |
| 4 | (14,8; 15,6] | 16 | 0,32 |
| 5 | (15,6; 16,4] | 16 | 0,32 |
| 6 | (16,4; 17,2] | 3 | 0,06 |
| 7 | (17,2; 18,0] | 1 | 0,02 |
| n=50 |
Примечание: fн – абсолютные частоты; p — относительные частоты
Если мы построим график, в котором по оси X отложим значения признака, а по оси У – абсолютную или относительную частоту, то получим график, который называется гистограммой.
Гистограмма – график, показывающий частоту попадания элементов выборки в соответствующий интервал группировки.
После этого по данным таблицы 4 строим гистограмму (рис.2).
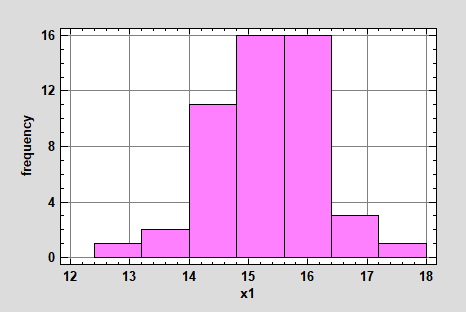
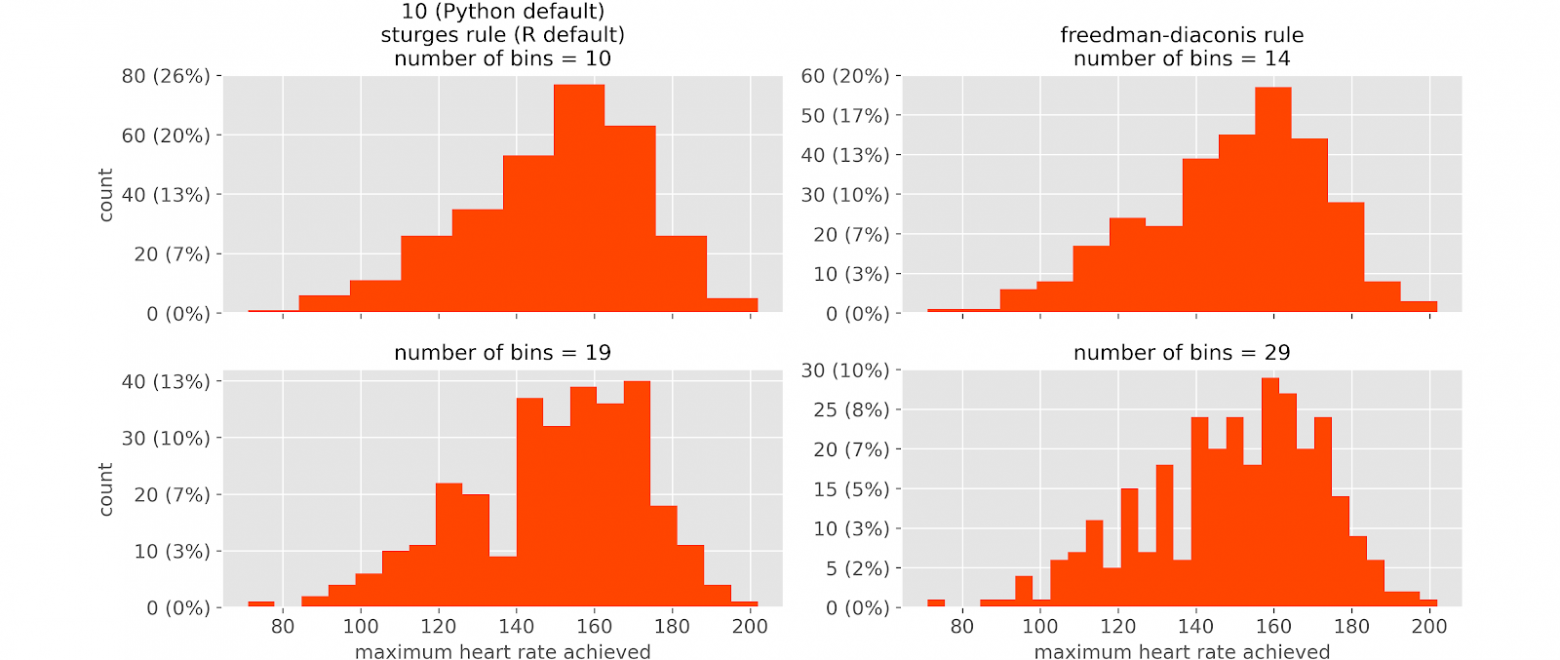
Достоинством гистограммы является наглядность представления экспериментальных данных. Однако по мнению Samuele Mazzanti внешний вид гистограммы сильно зависит от количества интервалов (рис. 3). Именно поэтому так важно определить оптимальное количество интервалов. В этом случае рекомендуется обратиться к табл.3.
Если нужно сравнить несколько выборок форма представления экспериментальных данных в виде гистограммы по мнению Samuele Mazzanti является не очень удачной. Это наглядно демонстрирует рис.4.
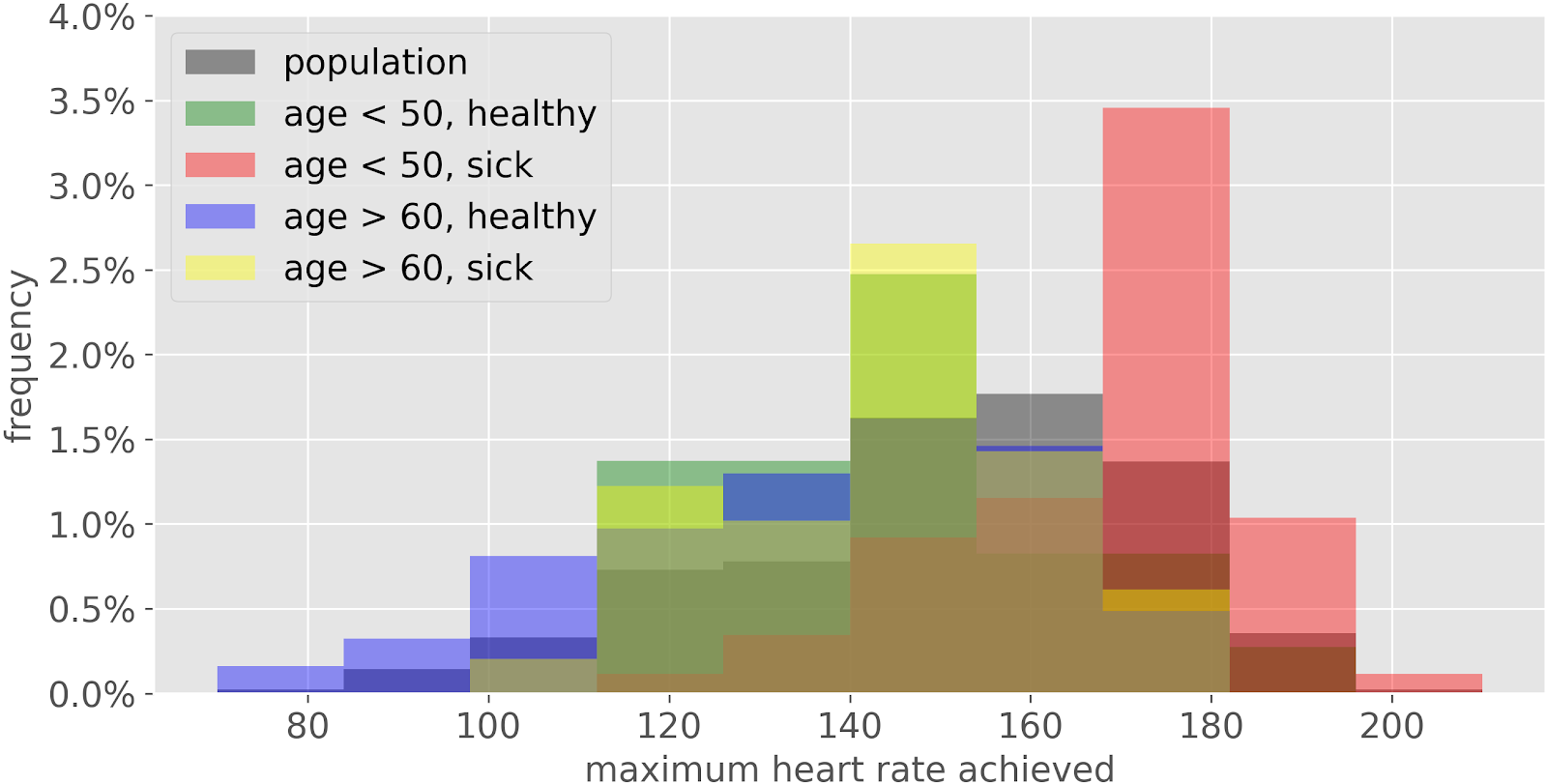
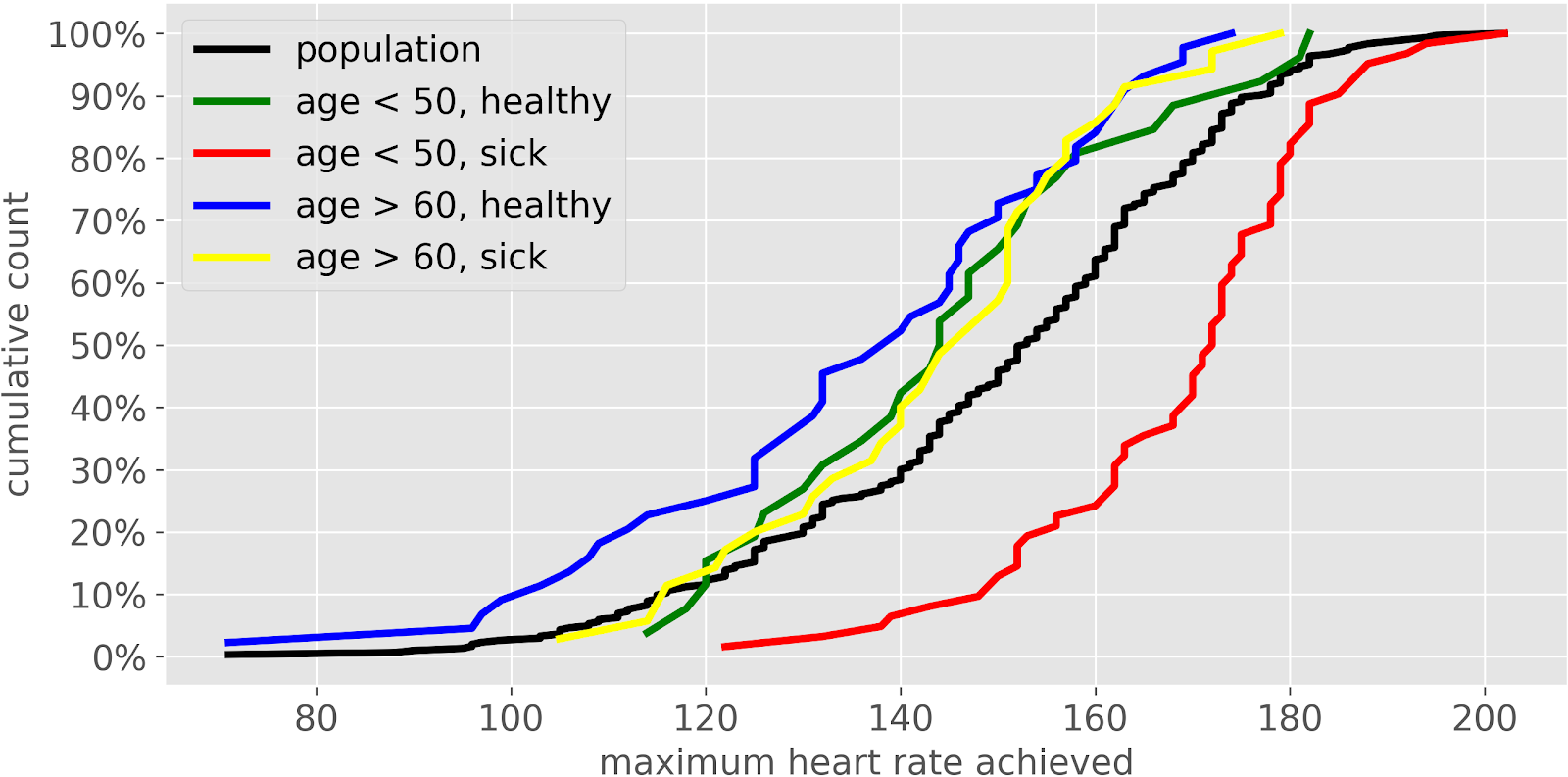
В связи с этим Samuele Mazzanti рекомендует при необходимости сравнивать несколько выборок использовать кумуляту (рис.5), так как наглядность кумуляты не зависит от количества интервалов и количества выборок.
Кумулята – график, полученный при соединении отрезками прямых точек, координаты которых соответствуют верхним границам интервалов группировки и накопленным частотам.
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
- Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.
С уважением, А.В. Самсонова
- Учебные пособия по статистике
- Видеоуроки по Statgraphics
- Введение в математическую статистику
- Генеральная совокупность и выборка
- Статистические шкалы
- Эмпирические распределения
- Числовые характеристики выборки
- Стандартная ошибка среднего арифметического
- Представление результатов исследования
- Точечное и интервальное оценивание числовых характеристик
- Элементы теории вероятностей
- Нормальный закон распределения (закон нормального распределения)
- Статистические гипотезы
- Критерии проверки статистических гипотез
- Критерии согласия
- Обоснование выбора критерия значимости
- Параметрические критерии
- Статистические операции в номинальной шкале
- Представление данных статистического анализа
- Корреляционный анализ
- Представление данных корреляционного анализа
- Регрессионный анализ
- Представление результатов регрессионного анализа