Генеральная совокупность и выборка

Кусок пиццы как пример репрезентативной выборки из генеральной совокупности

Генеральная совокупность и выборка (теория и практика)

Определения

Генеральная совокупность – совокупность всех значений признака, которая может быть получена при его измерении (исследовании). В качестве примера генеральной совокупности можно привести значения роста школьников старших классов в школе (рис.1).

Пример генеральной совокупности - рост мальчиков старших классов в школе. Пример выборки - рост мальчиков в одном из старших классов. — Рис. 1. Пример генеральной совокупности — рост мальчиков старших классов в школе. Пример выборки — рост мальчиков в одном из старших классов

Есть немного другое определение генеральной совокупности.

Генеральная совокупность – множество однородных, но индивидуально различимых объектов, имеющих хотя бы один общий признак, позволяющий их классифицировать, сравнивать друг с другом. Например, общим признаком корзины яблок является их масса. Каждое яблоко будет характеризоваться индивидуальным значением массы. Если мы измерим массу каждого яблока в корзине, мы получим совокупность всех значений признака, которая может быть получена при его измерении.

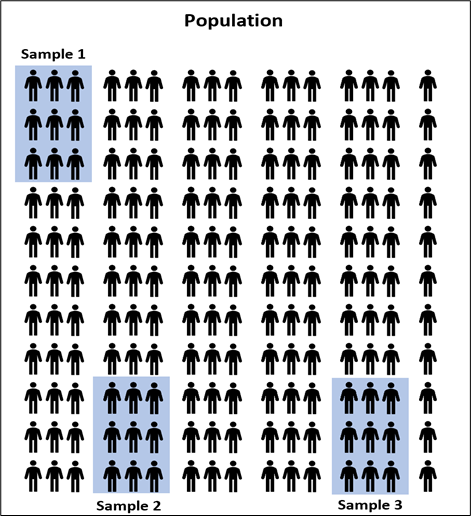
Выборка – часть генеральной совокупности, выбранная для исследования. Продолжая наш пример, корзина яблок – это выборка из всех яблок сада. Выборкой также являются значения роста мальчиков старших классов в одном из классов школы.

Объем выборки (n) – количество результатов измерений, взятых для исследования. Продолжая наш пример объем выборки – это количество яблок в корзине.

Более подробно о методах статистической обработки данных рассказано в книгах:

Требования к выборке

Чтобы по выборке можно было судить о генеральной совокупности должны выполняться следующие условия:

выборка должна быть репрезентативной (представительной), то есть выборка должна хорошо представлять генеральную совокупность (рис.2). Это обеспечивается в тех ситуациях, когда выборка является случайной, то есть любой объект имеет одинаковую вероятность попасть в выборку.

Рис.2. Примеры презентативных выборок и нерепрезентативной выборки

выборка должна быть однородной, то есть получена из одной генеральной совокупности (например, результаты спортсменов одного возраста, квалификации, специализации; рост солдат, участвующих в параде 9 мая (рис.3).

Пример однородной выборки - солдаты, участвующие в параде 9 мая — Рис. 3. Пример однородной выборки — солдаты, участвующие в параде 9 мая

Символы для обозначения генеральных параметров и их выборочных оценок

Чтобы различать параметры генеральной совокупности и числовые характеристики выборки используют различные символы (таблица 1

Таблица 1 — Обозначения параметров генеральной совокупности и выборки

Название характеристики	Генеральная совокупность	Выборка
Среднее арифметическое	μ	M или (x c чертой)
Дисперсия	σ²	S²
Стандартное отклонение	σ	S
Объем совокупности или выборки	N	n

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Лакин Г.Ф. Биометрия.- М.: Высшая школа, 1980.- 293 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.

С уважением, А.В. Самсонова