Модуль Юнга (модуль упругости)
Дано описание жизни и открытий английского ученого-экциклопедиста Томаса Юнга. Рассмотрена история открытия модуля Юнга и значение этого открытия для инженерных расчетов. Приведены значения модуля Юнга для некоторых материалов и элементов опорно-двигательного аппарата (ОДА) человека.
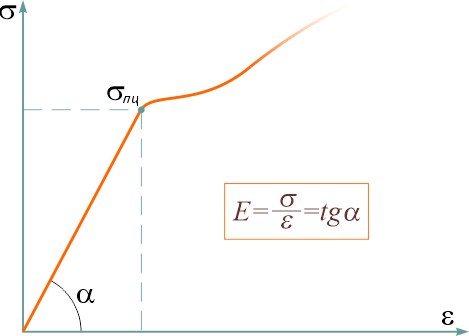
Модуль Юнга (модуль продольной упругости)
Прежде чем мы поговорим о модуле Юнга, несколько слов об его авторе – Томасе Юнге.
Томас Юнг (жизнь и открытия)
Томас Юнг (Thomas Young, 1773-1829) – один из выдающихся английских ученых-энциклопедистов (рис.1).

Нам он известен как физик, именем которого назван модуль упругости во время растяжения или сжатия тела. Однако Томас Юнг был очень разносторонним человеком. По профессии он был врачом, имел степень доктора медицины. Однако, он также достиг научных успехов в астрономии и механике, металлургии и ботанике, океанографии и филологии. Томас Юнг был полиглотом (владел 13 языками), серьезным знатоком музыки и искусным музыкантом, игравшим едва ли не на всех инструментах того времени, а также отличным живописцем (рис.2). Поэтому современники называли его: «The Last Man Who Knew Everything» — «Последний человек, который знает все». Несмотря на свои успехи в других областях науки, до конца жизни Томас Юнг продолжал работать врачом в одной из больниц Лондона.

Модуль Юнга (история открытия)
В отличие от Роберта Гука, который во многом предвосхитил многие открытия в области физики, однако в настоящее время они связываются с именами других ученых, Томасу Юнгу повезло более. Юнг описал характеристику упругости материала, которая стала известна как модуль Юнга, в своем «Курсе лекций по натуральной философии и механическому искусству». Книга была издана в 1807 году. Однако впервые понятие модуля упругости было использовано в экспериментах Джордано Риккати в 1782 году — на 25 лет раньше Томаса Юнга. Более того, идея модуля упругости описана в работе Леонгарда Эйлера, опубликованной в 1727 году, примерно за 80 лет до работы Томаса Юнга (Wikipedia).
Модуль Юнга (определение)
Модуль Юнга (синонимы: модуль продольной упругости, модуль нормальной упругости) — физическая величина, характеризующая способность материала (тела) сопротивляться растяжению или сжатию при упругой деформации.
Модуль Юнга (Е) измеряется в Паскалях. Он равен:
Е=σ÷ε (1),
где:
- σ — напряжение;
- ε — относительное удлинение образца.
Напряжение σ рассчитывается по формуле (2):
σ=F÷S (2),
где:
- F — сила,
- S — площадь поперечного сечения образца.
Относительное удлинение ε образца рассчитывается по формуле (3):
ε=Δl÷l (3),
где:
- Δl — удлинение образца,
- l — длина образца.
Чем больше численное значение модуля Юнга, тем больше сопротивление материала растяжению или сжатию при упругой деформации.
Следует отметить, что значение модуля Юнга зависит только от свойств материала, из которого изготовлен образец. Введение модуля Юнга впервые позволило предсказать деформацию образца, находящегося под известным напряжением, то есть определить относительное удлинение (ε):
ε = σ÷E (4)
До введения модуля Юнга инженеры должны были применять закон Гука (F = kΔl) для определения деформации (Δl) тела при известной нагрузке (F), где константа (k) является функцией как геометрии, так и материала образца. Поэтому нахождение k требовало физических испытаний для любого нового образца. В связи с тем, что значение модуля Юнга зависит только от свойств материала, а не от геометрии образца, использование этого показателя позволило совершить революцию в инженерных расчетах.
Численное значение модуля Юнга для материалов и элементов ОДА человека
В табл.1 представлены значения модуля Юнга для некоторых материалов и элементов ОДА человека. Из таблицы 1 следует, что из представленных в ней материалов наибольший модуль Юнга у стали, наименьший — у резины.
Из элементов ОДА человека наибольший модуль Юнга у бедренной кости. Он практически равен показателям железного дерева.
Таблица 1. Модуль упругости (Модуль Юнга) некоторых материалов и элементов ОДА человека
| Автор, год | Материал или элемент ОДА | Модуль упругости (E), МПа |
| Терегулов Ю.Э., Маянская С.Д., Терегулова Е.Т., 2017 | Эластин | 0,3 |
| Коллаген | 100 | |
| Дубровский В.И., Федорова В.Н., 2003 | Мышца в покое | 0,9 |
| Ершова А.И., 2018 | Бедренная кость | 27800 |
| Magnusson S.P. et al., 2003 | Ахиллово сухожилие | 800 |
| Maganaris C.N., Paul J.P., 2002 | Ахиллово сухожилие | 1200 |
| Maganaris C.N., Paul J.P., 1999 | Сухожилие передней большеберцовой мышцы | 1200 |
| Maganaris C.N., Narici, Reeves, 2004 | Сухожилие четырехглавой мышцы бедра | 1300 |
| Анурьев В. И., 2001 | Сосна | 8800 |
| Железное дерево | 32500 | |
| Резина | 5 | |
| Сталь | 190000-210000 |
Установлено, что под влиянием силовой тренировки модуль Юнга сухожилия четырехглавой мышцы бедра возрастает с 1300 до 2200 МПа. Это означает, что под влиянием силовой тренировки сухожилие четырехглавой мышцы бедра становится более жестким.
Литература
- Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В.И. Анурьев; 8-е изд., перераб. и доп. Под ред. И.Н. Жестковой. – М.: Машиностроение, 2001. — С. 34.
- Дубровский В.И., Федорова В.Н. Биомеханика. Учебник: М.: ВЛАДОС-ПРЕСС, 2003. – 672 с.
- Ершова А.И. Модули упругости и твердость кортикальной костной ткани: наноиндентирование образца бедренной кости // 75-я научная конференция студентов и аспирантов Белорусского государственного университета [Электронный ресурс] : материалы конф. В 3 ч. Ч. 1, Минск, 14–23 мая 2018 г. / Белорус. гос. ун-т, Гл. упр. науки ; редкол.: В. Г. Сафонов (пред.) [и др.]. – Минск : БГУ, 2018. – С. 14-18.
- Терегулов Ю.Э., Маянская С.Д., Терегулова Е.Т. Изменения эластических свойств артерий и гемодинамические процессы // Практическая медицина, № 2, 2017.- С. 14-20.
- Young T. Course of Lectures on Natural Philosophy and the Mechanical Arts. London: Taylor and Walton. 1807.
С уважением, А.В.Самсонова