Корреляционный анализ (теория и практика)
Корреляционный анализ – раздел математической статистики, исследующий зависимости между двумя или более случайными величинами.
Термин «Correlation» означает взаимосвязь, взаимоотношение.
История разработки корреляционного анализа
Еще Гиппократ обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенностью к заболеваниям существует определенная взаимосвязь. Однако термин «корреляция» был впервые применил французский палеонтолог Ж.Кювье в 1806 году в труде в труде «Лекции по сравнительной анатомии» Этот ученый вывел «закон корреляции частей и органов животных», позволяющий восстанавливать по найденным частям тела облик всего животного. Математическое обоснование метода предложено французским физиком Огюстом Браве (рис.1) в 1846 году.

Термин «корреляция» в математическую статистику ввел Фрэнсис Гальтон (рис.2) в 1888 году. Этот ученый добился больших успехов во многих областях науки: географии, метеорологии, криминалистике и психологии. Ему принадлежит первенство в создании первой погодной карты. Кроме того, он изобрел систему использования отпечатков пальцев для идентификации преступников.

Однако основным направлением его исследований была наследственность. С этой целью в 1884 году Фрэнсис Гальтон создал в Лондоне Антропометрическую лабораторию, которая представляла собой центр сбора данных о людях, которые принимали участие в исследовании. Благодаря этому ему удалось получить данные более чем о 10 000 человек.Для осмысления полученных данных Фрэнсис Гальтон разработал статистические методы: корреляционный и регрессионный анализы. Конечно, это было только начало статистического анализа. Тем не менее, в публикации 1888 года Фрэнсис Гальтон предложил показатель, который он назвал «индекс корреляции», и обозначил его буквой r. Этот показатель теперь называется «коэффициент корреляции». После Фрэнсиса Гальтона теорию корреляции активно разрабатывали Карл Пирсон и Чарльз Спирмен.
Функциональная зависимость и корреляция
Две случайные величины X и Y могут быть:
- связаны функциональной зависимостью (жестко, как зависимость переменных в математическом анализе);
- независимыми;
- связаны стохастической (вероятностной зависимостью) при которой изменение одной величины влечет изменение распределения другой.
Функциональная зависимость
На рис.3 приведен график линейной функции. В области физической культуры и спорта можно привести много примеров функциональной зависимости. Например, скорость бега (V) линейно зависит от длины (L) и частоты шагов (ν): V = L∙ν.
Стохастическая (вероятностная зависимость)
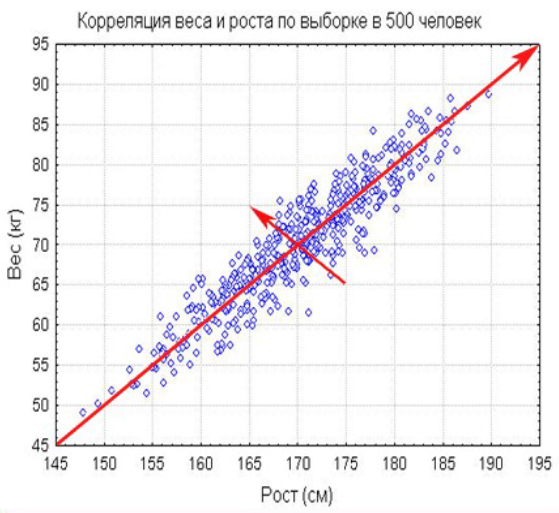
Примером стохастической (корреляционной зависимости) является зависимость веса человека от роста (рис. 4).
Коэффициент корреляции
В качестве меры связи между случайными величинами используется коэффициент корреляции. Коэффициент корреляции для генеральной совокупности обозначается ρ. Однако, как правило, он неизвестен. Поэтому он оценивается по экспериментальным данным, представляющим выборку объема n, полученную при совместном измерении двух переменных (признаков) X и Y. Коэффициент корреляции, определяемый по выборочным данным называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r. Наиболее часто в качестве оценок генерального коэффициента корреляции используются:
- коэффициент корреляции Пирсона (r);
- коэффициент корреляции Спирмена (rs);
- коэффициент корреляции Кендалла (τ).
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта (электронная книга)
- Математическая статистика в спортивных исследованиях (электронная книга)
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
Коэффициент корреляции Пирсона (r)
Коэффициент корреляции, который теперь называется коэффициент корреляции Пирсона был разработан английским математиком Карлом Пирсоном (рис.5) в 1896 году (Zorich J.N., 2025).

Формула, по которой рассчитывается коэффициент корреляции Пирсона выгладит следующим образом:
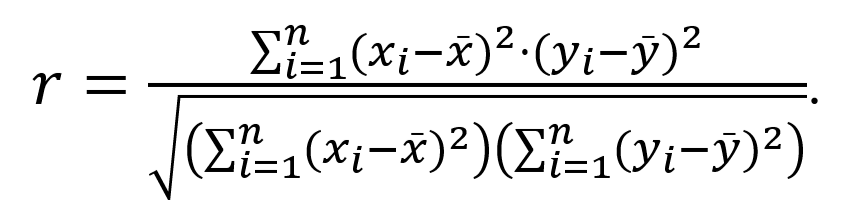
Расчет коэффициента корреляции Пирсона возможен, если будут выполнены следующие условия:
- Экспериментальные данные должны быть представлены в только в интервальной шкале или шкале отношений.
- Распределение экспериментальных данных подчиняется нормальному закону.
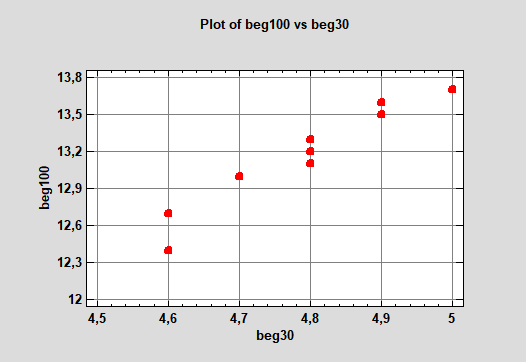
- Предполагается линейная зависимость между случайными величинами X и Y. Чтобы визуально представить эту зависимость нужно построить корреляционное поле. С этой целью строится график, по оси X откладываются значения одного признака, а по оси Y — соответствующие ему значения второго признака (рис. 6). По этому графику можно судить насколько распределение точек близко к прямой линии.
Коэффициент корреляции Спирмена (rS)
В 1904 году Чарльз Эдвард Спирмен (рис. 7), английский психолог, разработал коэффициент ранговой корреляции, который носит теперь его имя.

Для расчета коэффициента корреляции Спирмена используется формула:
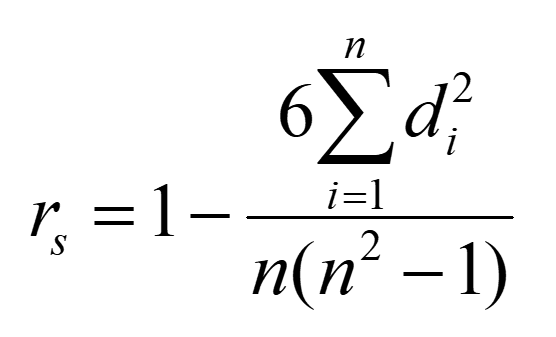
Требования к исходным данным менее строгие, а именно:
- Данные могут быть представлены в порядковой, интервальной шкале или шкале отношений.
- Допускается любой закон распределения случайных величин X и Y.
- Между случайными величинами X и Y должна существовать монотонно-возрастающая или монотонно-убывающая зависимость.
Коэффициент корреляции Кендалла
В 1938 году английский статистик Морис Джордж Кендалл (рис. 8), разработал коэффициент корреляции (τ) , который носит теперь его имя.

Условия применения:
- Обе переменные представлены в порядковой шкале.
- Любой закон распределения переменных X и Y.
Коэффициент корреляции рассчитывается по формуле:
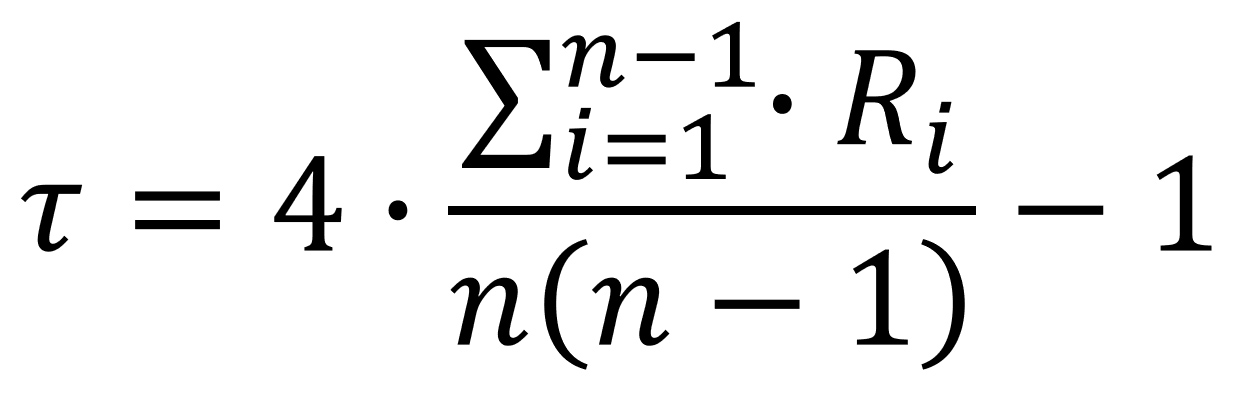
Ri – число рангов во втором вариационном ряду, бóльших, чем данное ранговое число и расположенных ниже него; n – объём выборки.
Идея расчета коэффициента корреляции Кендалла заключается в следующем. Предполагается, что корреляция между двумя переменными будет высокой, если наблюдения имеют близкие по значению ранги и низкой, если переменные имеют сильно отличающиеся ранги. Применение коэффициента корреляции Кендалла является более предпочтительным, если в исходных данных имеются выбросы.
Пример расчета коэффициента корреляции Кендалла. Имеем исходную таблицу (таблица 1)
Таблица 1
| № | Ф.И. | Rx | Ry | Ri |
| 1 | Катя Г. | 1 | 5,5 | 3 |
| 2 | Даша В. | 2 | 5,5 | 3 |
| 3 | Маша Д. | 3 | 2,5 | 5 |
| 4 | Игорь М. | 4 | 1 | 6 |
| 5 | Яша Б. | 5 | 5,5 | 3 |
| 6 | Боря Л. | 6 | 10 | 0 |
| 7 | Зина С. | 7 | 8,5 | 0 |
| 8 | Лёня А. | 8 | 5,5 | 11 |
| 9 | Аня Л. | 9 | 8,5 | 0 |
| 10 | Вася Р. | 10 | 2,5 | 0 |
| сумма | 21 |
Для расчета коэффициента корреляции Кендалла необходимо расчетную таблицу перегруппировать по возрастанию рангов первой переменной (Rx). Последний столбец (R) заполняется следующим образом: ниже Кати Г. (Ry = 5,5) (выделено оранжевым цветом) имеется 3 ранга Ry, больших, чем у Кати Г. (5,5); ниже Даши В. (Ry = 5,5) имеется 3 ранга Ry, больших, чему Даши (5,5); ниже Маши Д. (Ry = 2,5) имеется 5 рангов Ry, больших, чем у Маши Д. (2,5). Таким образом значение коэффициента корреляции Кендалла равно:
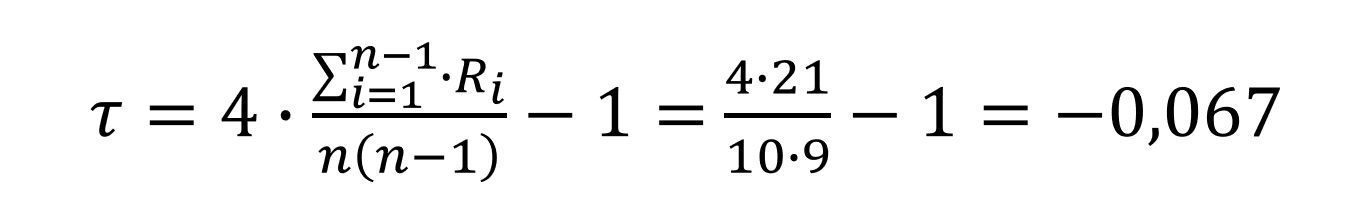
Свойства оценок коэффициентов корреляции
Рассчитанные коэффициенты корреляции могут принимать значения от -1 до +1.
- Если коэффициент корреляции равен: r =+1 и r = -1, это означает, что случайные величины X и Y связаны жесткой линейной зависимостью.
- Если r ≠ 0, то чем ближе |r| к единице, тем сильнее линейная зависимость случайных величин X и Y.
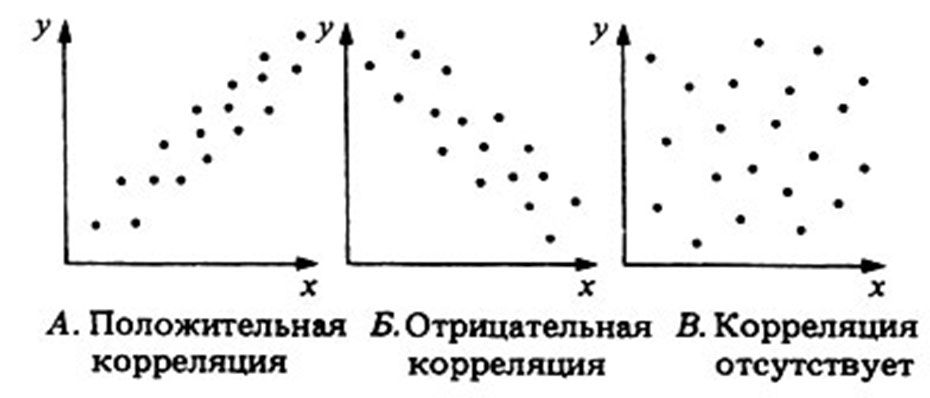
- Если коэффициент корреляции положительный (r > 0) – это означает, что между случайными величинами X и Y существует положительная корреляция (или другими словами положительная корреляционная зависимость). Примером положительной корреляционной зависимости является увеличение результата прыжка в длину с увеличением силы мышц ног (рис.9А).
- Eсли коэффициент корреляции отрицательный (r < 0) – это означает, что между случайными величинами X и Y существует отрицательная корреляция (или другими словами отрицательная корреляционная зависимость). Примером отрицательной корреляционной зависимости является уменьшение результата пробегания 100 м с увеличением силы мышц ног (рис. 9Б)
- Если коэффициент корреляции равен нулю (r = 0) – это означает, что корреляции нет; случайные величины X и Y некоррелированы (рис. 9В). Другими словами, это означает, что между случайными величинами X и Y нет взаимосвязи.
Геометрическая интерпретация коэффициента корреляции
- Корреляция считается положительной, если график имеет выраженное направление из левого нижнего угла в правый верхний угол и с увеличением значений одной переменной другая также увеличивается;
- Корреляция считается отрицательной, если график имеет направление из левого верхнего угла в правый нижний, и с увеличением одной переменной, другая уменьшается;
- Корреляция отсутствует, когда у корреляционного облака нет четко выраженного направления, точки рассеиваются далеко от воображаемой прямой и нельзя сказать, что с увеличением одной переменной другая уменьшается или увеличивается.
Значимость коэффициента корреляции
Коэффициент корреляции между случайными величинами X и Y для генеральной совокупности как правило, неизвестен. Однако его можно оценить, рассчитав выборочный коэффициент корреляции (коэффициент корреляции Пирсона или Спирмена). Но при заменяя генеральную совокупность выборкой при оценке коэффициента корреляции допускается ошибка. Поэтому важно оценить значимость (достоверность) рассчитанного коэффициента корреляции.
Например, в эксперименте участвовало 10 человек (корреляционное поле представлено на рис.6). Оценивалась взаимосвязь между результатами в беге на 30 м и 100 м. Получен коэффициент корреляции r = 0,611. Чтобы оценить значимость коэффициента корреляции нужно сравнить его с критическим, величина которого зависит от объема выборки и уровня значимости. Если фактическое значение коэффициента корреляции больше, чем критическое, это означает, что коэффициент корреляции достоверен (значим). В нашем случае критическое значение коэффициента корреляции при n= 10 и α = 0,05 составляет r0,05 =0,632 (в таблице 1 это значение выделено жирным шрифтом). Из этого следует, что рассчитанный коэффициент корреляции статистически недостоверен. Приводить его в своих исследованиях нежелательно.
Таблица 1 — Критические значения коэффициента корреляции Пирсона
| n | 0,05 | 0,01 | 0,001 |
| 3 | 0,9969 | 0,999877 | 0,99999877 |
| 4 | 0,950 | 0,9900 | 0,9990 |
| 5 | 0,878 | 0,9597 | 0,99114 |
| 6 | 0,811 | 0,9172 | 0,9741 |
| 7 | 0,754 | 0,875 | 0,9509 |
| 8 | 0,707 | 0,834 | 0,9244 |
| 9 | 0,666 | 0,798 | 0,898 |
| 10 | 0,632 | 0,765 | 0,872 |
| 20 | 0,444 | 0,561 | 0,679 |
| 30 | 0,361 | 0,463 | 0,570 |
| 40 | 0,312 | 0,402 | 0,501 |
| 50 | 0,279 | 0,361 | 0,451 |
В итоговой таблице необходимо указать объем выборки, чтобы читающий мог оценить значимость (достоверность) вычисленных коэффициентов корреляции.
Литература
- Катранов, А.Г. Компьютерная обработка данных экспериментальных исследований / А.Г. Катранов, А.В. Самсонова /Учебное пособие.– СПб: СПбГАФК им. П.Ф. Лесгафта, 2005.– 132 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ./ /Под ред. В.С.Иванова. М.: Физкультура и спорт, 1990.– 176 с.
- Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.
- Zorich J.N. The History of Correlation.- CRC Press 4 Park Square, Milton Park, Abingdon, Oxon, OX14 4RN, 2025.
- Учебные пособия по статистике
- Видеоуроки по Statgraphics
- Введение в математическую статистику
- Генеральная совокупность и выборка
- Статистические шкалы
- Эмпирические распределения
- Числовые характеристики выборки
- Стандартная ошибка среднего арифметического
- Представление результатов исследования
- Точечное и интервальное оценивание числовых характеристик
- Элементы теории вероятностей
- Нормальный закон распределения (закон нормального распределения)
- Статистические гипотезы
- Критерии проверки статистических гипотез
- Критерии согласия
- Обоснование выбора критерия значимости
- Параметрические критерии
- Статистические операции в номинальной шкале
- Представление данных статистического анализа
- Корреляционный анализ
- Представление данных корреляционного анализа
- Регрессионный анализ
- Представление результатов регрессионного анализа