Этапы и методы факторного анализа
Рассмотрены первые два этапа факторного анализа (постановка проблемы, отбор и измерение переменных для исследования, подготовка матрицы исходных данных, ковариационной или корреляционной матрицы и выбор метода факторного анализа), а также основные методы факторного анализа (метод главных компонент, метод максимального правдоподобия, метод главных факторов и центроидный метод).
Этапы и методы факторного анализа
При проведении факторного анализа исследователю предстоит ответить на следующие вопросы, рис.1.
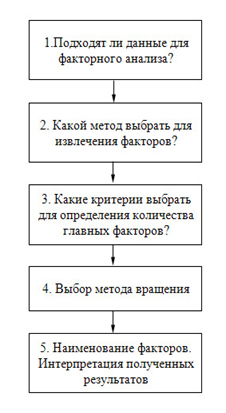
В связи с этим, можно считать, что факторный анализ состоит из следующих этапов:
- Постановка проблемы, отбор и измерение переменных для исследования. Подготовка матрицы исходных данных. Подготовка ковариационной или корреляционной матрицы.
- Выбор метода факторного анализа.
- Выделение первоначальных факторов. Определение количества необходимых факторов.
- Выбор метода вращения. Вращение факторов.
- Содержательная интерпретация результатов.
Рассмотрим, как выполнить первые два пункта факторного анализа.
Постановка проблемы, отбор и измерение переменных для исследования. Подготовка матрицы исходных данных. Подготовка ковариационной или корреляционной матрицы
Для осуществления перехода от исходных переменных к меньшему количеству факторов, необходимо использовать внутреннюю структуру матриц. Промежуточными звеньями при переходе от матрицы данных к факторной матрице служат корреляционные матрицы.
Что представляют собой эти матрицы? Наиболее важной матрицей для проведения статистических процедур является матрица данных.
Матрица данных
Матрица данных формируется следующим образом. Результаты исследований заносятся в таблицу, где объекты исследования (N) образуют строки матрицы, а переменные (n) ее столбцы. Матрица обозначается заглавной буквой латинского алфавита. Матрица может рассматриваться, как набор векторов. Каждый столбец матрицы – это вектор-столбец, а каждая строка матрицы – вектор-строка.
Матрица взаимосвязей
Второй важной матрицей факторного анализа является матрица взаимосвязей. Если между переменными существует взаимосвязь, то они могут быть представлены матрицей ковариаций или матрицей корреляций. С вычисления корреляционной или ковариационной матрицы начинается факторный анализ.
Для факторного анализа необходимо, чтобы данные исходной матрицы были измерены в интервальной шкале или шкале отношений, так как метод рассчитан, в основном, на непрерывные переменные, соответствующие нормальному закону распределения. В социальных и биологических науках, в экономических исследованиях нормальное распределение измеряемых признаков – это скорее исключение, чем правило. Поэтому для того, чтобы подготовить непараметрические признаки к процедуре факторного анализа их ранжируют, например, в шкале Ликерта[1], а затем в качестве переменных используются ранги, что, в общем, не совсем корректно. В последнее время появилась возможность обработки порядковых данных с помощью категориального анализа главных компонент. Применение такого анализа возможно в статистическом пакете SPSS.
Для выполнения факторного анализа переменные стандартизируют. К стандартизации данных относятся их центрирование и нормирование. С помощью стандартизации начало координат и единица измерения фиксируются, что позволяет привести значения переменных к более удобной форме. У стандартизированных переменных среднее значение равно нулю, а дисперсия (и стандартное отклонение) равно единице.
В компьютерных пакетах статистического анализа в основном используется матрица корреляций, как более удобная, но в отдельных случаях может быть применена и матрица ковариаций. Для получения корреляционной матрицы рассчитывается коэффициент корреляции Пирсона.
Расчет параметрического коэффициента корреляции Пирсона подразумевает, что данные для анализа должны соответствовать нормальному распределению. Однако некоторые авторы считают, что поскольку факторный анализ включает в себя обнаружение взаимосвязей между большим количеством различных данных, допущения в отношении нормальности не так уж важны. Из методов факторного анализа наиболее требователен к нормальности распределения данных — метод максимального правдоподобия.
Как матрица ковариаций, так и матрица корреляций являются симметрическими, их элементы симметричны относительно главной диагонали. Отличием является то, что в матрице ковариаций на главной диагонали стоят дисперсии данных, а вне диагонали – коэффициенты ковариаций исследуемых переменных, а в корреляционной матрице на главной диагонали находятся единичные коэффициенты корреляций, или же значения дисперсий, равных единице.
Полученная корреляционная матрица оценивается с точки зрения ее пригодности к проведению факторного анализа. Для решения этой задачи существует несколько критериев. Один из наиболее доступных критериев – величина взаимосвязи между переменными. Если коэффициенты корреляции низкие (менее 0,3) – это свидетельствует о нецелесообразности проведения факторного анализа. Это означает, что при наличии большого количества низких коэффициентов корреляции факторный анализ становится проблематичным, так как исходные данные слишком разнородны.
В отдельных статистических пакетах, к примеру, в SPSS присутствует критерий сферичности Бартлетта, который проверяет нулевую гипотезу об отсутствии корреляций в генеральной совокупности и критерий адекватности выборки Кайзера-Мейера-Олкина (КМО), который позволяет проверить насколько корреляцию между переменными можно объяснить другими переменными (факторами).
Третьей важной матрицей является матрица факторных нагрузок (факторная матрица).
Выбор метода факторного анализа
На этапе факторизации производится выбор модели факторного анализа. Существуют два подхода (алгоритма в расчетах) при выполнении процедуры факторного анализа.
При использовании первого подхода вначале устанавливается количество факторов, затем подбираются значения общностей, таким образом, чтобы ранг матрицы приближался к числу факторов (m). Такой алгоритм используется в методе главных компонент и методе максимального правдоподобия.
При применении второго подхода вначале определяются общности, затем – число факторов. Такой алгоритм используется в методе главных факторов и центроидном методе.
Чаще всего в исследованиях применяется метод главных компонент и метод главных факторов, поскольку они наиболее распространены в различных статистических пакетах.
Метод главных компонент по своей модели и цели исследования отличается от факторного анализа. Он применяется, как отдельный метод, если целью исследования является снижение размерности матрицы исходных данных. И в то же время он может быть начальным этапом факторного анализа, вспомогательным звеном для осуществления отбора главных факторов. Практически все статистические пакеты имеют по умолчанию в функции факторного анализа метод главных компонент.
В методе главных компонент ищут некоррелированные независимые комбинации переменных, дисперсии которых обладают особым свойством, они расположены в убывающем порядке. Другими словами, целью метода главных компонент является нахождение такого базиса, в котором исследуемые переменные могли бы быть представлены меньшим количеством переменных, называемых компонентами (факторами). Геометрически нахождение главных компонент сводится к переходу к новой ортогональной системе координат.
Исходной матрицей для анализа в методе главных компонент является корреляционная матрица с единичными коэффициентами корреляции на главной диагонали (рис.2).
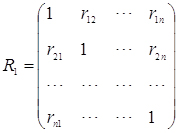
Литература
Самсонова, А.В. Факторный анализ в педагогических исследованиях в области физической культуры и спорта: учеб. пособие / А.В. Самсонова, И.Э. Барникова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт-Петербург.– СПб.: [Б.и.], 2013. — 90 с.
С уважением, А.В. Самсонова
[1] Шкала Ликерта — психометрическая шкала. Часто используется в опросниках и анкетах (разработана в 1932 году Ренсисом Ликертом). При работе со шкалой испытуемый оценивает степень своего согласия или несогласия с суждением. Обычно используется пять градаций от «полностью согласен» до «не согласен». (http://ru.wikipedia.org/wiki/).