Элементы теории веоятностей

Элементы теории вероятностей

Случайные величины

Определение и пример

Случайной величиной (с.в.) называется величина, которая в результате статистического испытания может принять то или иное значение, причем не известно заранее, какое именно.

Случайные величины обозначаются большими буквами из конца латинского алфавита: X, Y, Z. Конкретные возможные значения случайной величины обозначаются маленькими буквами – x, y, z.

Пример 1. Случайная величина Х – время пробегания дистанции 100 м. Значением случайной величины (х) является конкретный результат в беге на 100 м, например – 13,0 с.

Случайные величины делятся на дискретные и непрерывные.

Дискретные и непрерывные случайные величины

Случайная величина называется дискретной если множество ее значений конечно или счетно (может быть занумеровано натуральными числами, т.е.1,2,3 и т.д.).

Пример 2: количество попаданий в кольцо из 10 штрафных бросков (конечное); количество отжиманий (счетное).

Непрерывной называют случайную величину, которая может принимать любые значения из некоторого промежутка. Число значений непрерывной случайной величины бесконечно.

Пример 3. Непрерывными случайными величинами является рост, вес, время прохождения дистанции, результат прыжка и т.д.

Более подробно о методах статистической обработки данных рассказано в книгах:

Вероятность события

Классическое определение вероятности

Вероятностью Р (А) наступления события А является отношение количества исходов, благоприятствующих наступлению события А к количеству возможных исходов.

Пример 4. Вероятность выпадения цифры 5 при бросании игральной кости равна: Р (х=5)=1/6.

Статистическое определение вероятности

Классическое определение вероятности имеет ограниченное применение, поэтому более распространено статистическое определение вероятности.

Относительной частотой события А называют отношение m опытов, в которых появилось событие А к общему числу n проведенных опытов.

Английские математики Ж. Бюффон и К. Пирсон сравнивали относительную частоту и вероятность появления герба при бросании монеты. Они показали, что при увеличении количества опытов относительная частота приближается к вероятности события (табл. 1)

n	4040	12000	24000
P (A)	0,5080	0,5016	0,5005

Законы распределения случайных величин

Определение и пример

Законом распределения случайной величины называется всякое соответствие, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Законы распределения дискретной случайной величины

Дискретная случайная величина будет полностью описана, если каждому ее значению поставить в соответствие вероятность этого значения.

Примером закона распределения дискретной случайной величины является биномиальный закон.

Пример 5. Баскетболист выполняет серию из 10 штрафных бросков. Найти вероятности того, что в данной серии бросков баскетболист поразит кольцо: 0, 1, 2…10 раз, если вероятность попадания с одной попытки равна P=0,5.

Для описания этого события применим биномиальный закон (табл.2).

Таблица 2. Закон распределения случайной величины Х

Х	0	1	2	3	4	5	6	7	8	9	10
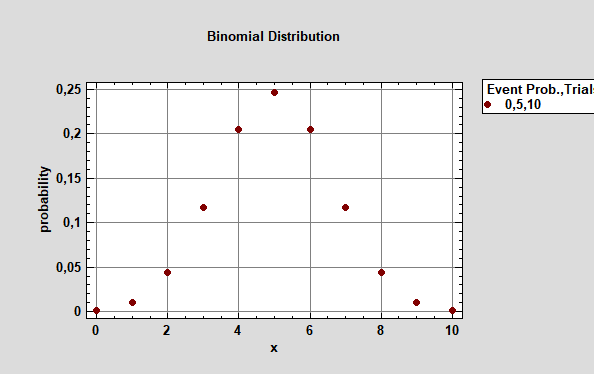
Р	0,001	0,010	0,044	0,017	0,205	0,246	0,205	0,117	0,044	0,010	0,001

Из табл.2 следует, что вероятность попадания в кольцо 5 раз из 10 бросков максимальная, она равна P=0,246. Вероятность попадания в кольцо 10 раз, как и вероятность всех промахов минимальная. Она равна Р=0,001.

График закона распределения дискретной случайной величины представлен на рис. 1. Такой график называется полигоном.

Рис.1. График распределения дискретной случайной величины

Закон распределения непрерывной случайной величины

Основным законом распределения непрерывной случайной величины является плотность распределения вероятностей (или плотность распределения) – f_x(x). Плотность распределения называют дифференциальным законом распределения.

Свойства функции плотности распределения:

Плотность распределения вероятностей – функция неотрицательнаяf_x(x)>=0.
Вероятность попадания любой случайной величины в интервал от до + равен 1 (достоверное событие).

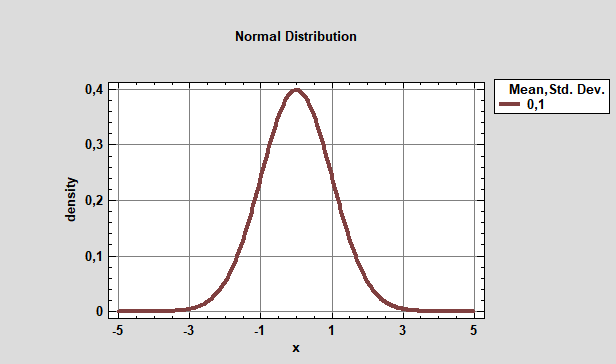
На рис. 2 представлен график плотности распределения непрерывной случайной величины (среднее арифметическое равно 0, стандартное отклонение – 1) на примере нормального распределения.

Распределение любой случайной величины (дискретной или непрерывной) может быть описано функцией распределения F_x(x), которую называют интегральным законом распределения.

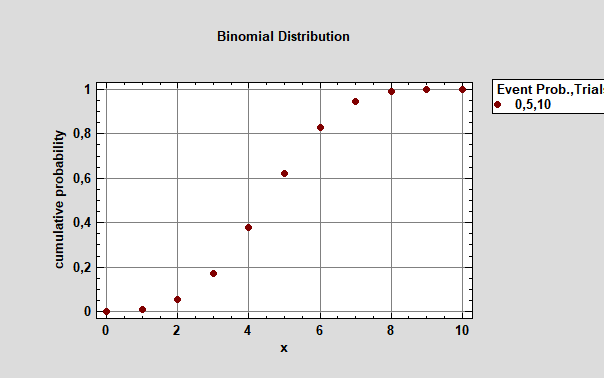
В случае распределения дискретной случайной величины функция распределения представляет собой возрастающую ступенчатую функцию со скачками в х_1,х_2,_X_3…_Xn_.(рис.3).

Рис.3. График функции распределения дискретной случайной величины

Свойства функции распределения:

Функция распределения принимает значение на интервале 0,1.
Функция распределения является неубывающей функцией.

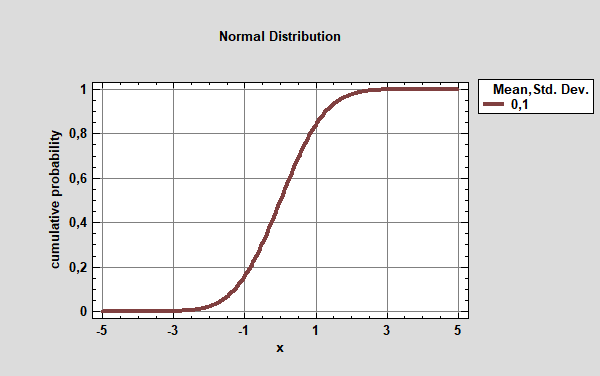
В случае распределения непрерывной случайной величины функция распределения представляет собой возрастающую функцию, которая принимает значения от 0 до 1. (рис.4).

Рис. 4. График функции распределения непрерывной случайной величины

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.