Факторный анализ. Направления применения и неиспользованные возможности

В статье А.В.Самсоновой Факторный анализ. Направления применения и неиспользованные возможности показано, что факторный анализ (ФА) позволяет решать целый ряд исследовательских задач, однако некоторые его возможности используются крайне редко. В большинстве случаев авторы ограничиваются приведением таблицы факторных нагрузок после вращения и анализом выделенных факторов. Значительно реже ФА используется для исследования динамики факторной структуры. Еще меньше публикаций, в которых на основе ФА выявляются наиболее информативные тесты. И совсем мало статей, в которых ФА применяется для анализа проявления индивидуальных способностей спортсменов.

Самсонова, А.В. Факторный анализ. Направления применения и неиспользованные возможности /А.В. Самсонова //Вестник Балтийской Педагогической Академии.- 2005.- вып. 62.- С. 67-75

Самсонова А.В.

ФАКТОРНЫЙ АНАЛИЗ. НАПРАВЛЕНИЯ ПРИМЕНЕНИЯ И НЕИСПОЛЬЗОВАННЫЕ ВОЗМОЖНОСТИ

ВВЕДЕНИЕ

Факторный анализ, как метод исследования, позволяет решать целый ряд исследовательских задач. Анализ статей в журнале «Теория и практика физической культуры» с 1970 по 2004 г.г. показывает, что очень редко используются все его возможности. В большинстве случаев авторы ограничиваются приведением таблицы факторных нагрузок после вращения и анализом выделенных факторов. Значительно реже (44%) факторный анализ используется для исследования динамики факторной структуры. Еще меньше публикаций (22%), в которых на основе факторного анализа выявляются наиболее информативные тесты. И совсем мало статей (5%), в которых факторный анализ применяется для анализа проявления индивидуальных способностей спортсменов. Нами не обнаружены исследования, посвященные анализу факторной модели результата. В то же время, современные статистические пакеты предоставляют богатые возможности для такого анализа.

Цель настоящей публикации состояла в демонстрации на конкретном примере статьи, посвященной факторному анализу, возможностей данного метода.

Факторный анализ структуры скоростных способностей девочек 12-13 лет

Целью исследования явилось изучение структуры скоростных способностей девочек, специализирующихся в спринтерском беге.

В исследовании были поставлены следующие задачи:

1. определить факторную структуру скоростных способностей девочек 12-13 лет;
2. определить наиболее информативные тесты;
3. выявить испытуемых, обладающих лучшими и посредственными показателями в проявлении скоростных способностей;
4. определить факторную модель комбинации способностей для достижения результата в беге на 100 м;

МЕТОДИКА

В исследовании принимали участие 12 девочек 12-13 лет, специализация – спринтерский бег. С использованием индуктивного канала связи регистрировались следующие показатели (переменные), табл.1.

lat – время от сигнала стартового пистолета, до отрыва рук от опоры, мс;

mot – время от сигнала стартового пистолета до отрыва впередистоящей ноги от опоры, мс;

t1-t8 – время пробегания пятиметровых отрезков, соответственно: первого, второго, третьего, четвертого, пятого, шестого, седьмого, восьмого, мс;

t100 – время пробегания 100 м, с.

Таблица 1

Результаты тестирования времени реакции и времени пробегания 5 м отрезков, девочки 12-13 лет

Полученные результаты были обработаны с использованием статистических пакетов STATGRAPHICS plus for Windows и SPSS. Факторизация корреляционной матрицы производилась посредством метода главных компонент.

РЕЗУЛЬТАТЫ

На первом этапе определялись собственные числа и степень влияния каждого фактора на полную дисперсию выборки (табл.2). Следует отметить, что степень, с которой каждый фактор объясняет полную дисперсию, представлена в %. Этот показатель получается делением собственного числа на количество всех переменных. На первом этапе выполнения факторного анализа было выделено 11 факторов, что соответствует числу переменных, участвующих в проведенном анализе.

Таблица 2 — Результаты проведения первого этапа факторного анализа

На втором этапе определялось число факторов, которые будут в дальнейшем подвергнуты анализу. Чаще всего (Масальгин Н.А., Медведев А.С., 1991; Дюк В., 1997; Бююль А., Цефель П., 2001) отбираются факторы, собственные числа которых не менее единицы (табл. 2). В данном случае таких факторов три. Первый фактор (собственное число 5,57) объясняет 50,6% полной дисперсии выборки; второй фактор (собственное число 2,49) – 22,6% полной дисперсии выборки; третий фактор (собственное число 1,53) – 13,9 % полной дисперсии выборки. Таким образом, выделено три фактора, объясняющих 87,3% полной дисперсии выборки.

Для решения первой задачи исследования – выявления факторной структуры скоростных способностей девочек 12-13 лет было выполнено вращение матрицы факторных нагрузок посредством варимакс-критерия (табл 3).

Таблица 3 — Матрица факторных нагрузок после процедуры вращения

Анализ матрицы факторных нагрузок после вращения свидетельствует о том, что в первом факторе высокие значения имеют факторные нагрузки для переменных: t4 (0,680), t5 (0,924), t6 (0,878) t7 (0,836), t8 (0,913) и t100 (0,875), они выделены жирным шрифтом. Эти переменные характеризуют скоростную способность, называемую скоростью выполнения движений. Во втором факторе высокие значения имеют факторные нагрузки для переменных: lat (0,922), mot (0,575) и t1 (0,883), которые характеризуют способность к быстрой реакции на сигнал спортсменок. В третьем факторе высокие значения имеют факторные нагрузки для переменных: t2 (0,976) и t3 (0,819). По-видимому, этот фактор характеризует способность к быстрому набору скорости.

Таким образом, выделено три фактора, характеризующих скоростные способности девочек 12-13 лет.

Понятие структура подразумевает не столько определение элементов системы (в данном случае выделение факторов), сколько установление взаимосвязей между ними. Следует отметить, что такой анализ почти никогда не проводится, и авторы ограничиваются только интерпретацией выделенных факторов. Для изучения этого вопроса обратимся к рис. 1 и рис. 2. На рис.1 представлена проекция исследуемых объектов (испытуемых) на плоскость первого и второго факторов. Судя по конфигурации облака точек можно сделать вывод, что между этими факторами нет корреляции. Следовательно, наши данные подтверждают результаты, полученные В.М.Зациорским (1969), которые свидетельствуют о том, что между способностью быстро реагировать и способностью быстро бегать нет взаимосвязи.

В то же время результаты, представленные на рис.2, свидетельствуют о том, что между первым и третьим фактором наблюдается существенная нелинейная зависимость. Таким образом, полученные результаты не подтверждают гипотезы В.М.Зациорского (1969) о том, что между способностью к быстрым движениям и способностью быстро набирать скорость не существует взаимосвязи.

Между способностью быстро реагировать на сигнал (фактор 2) и способностью быстро набирать скорость (фактор 3) также не обнаружено взаимосвязи.

Следовательно, факторная структура скоростных способностей девочек 12-13 лет определяется тремя факторами: первый фактор характеризует скорость выполнения движений, второй фактор характеризует способность к быстрой реакции на сигнал и третий фактор характеризует скоростную способность к быстрому набору скорости. Между первым и вторым фактором, а также вторым и третьим не наблюдается выраженной взаимосвязи, в то время как между первым и третьим фактором существует явная взаимосвязь.

Анализ матрицы факторных нагрузок (табл.3) может быть использован для решения второй задачи исследования – выявления информативных тестов. Переменная, имеющая максимальную нагрузку на фактор, является наиболее информативной в проявлении данного фактора.

Полученные результаты свидетельствуют о том, что способность бежать максимально быстро лучше всего характеризует переменная t5 (время пробегания пятого пятиметрового отрезка). Ее нагрузка на первый фактор равна 0,924542. Наиболее информативным показателем скорости реакции является латентное время реакции (переменная lat ). Ее нагрузка на второй фактор составляет 0,922842. Наиболее информативным показателем, характеризующим способность быстро набирать скорость, является переменная t2 (0,97646).

Таким образом, вместо 11 тестов (переменных) для оценки скоростных способностей девочек можно выбрать три теста: время от сигнала стартового пистолета до отрыва рук (способность к быстрому реагированию на сигнал), время пробегания второго отрезка дистанции (способность к быстрому набору скорости) и время пробегания пятого пятиметрового отрезка (способность к быстрому бегу).

Третья задача исследования состояла в выявлении спортсменок, обладающих лучшими и посредственными скоростными способностями. В таблице 4 приведены факторные значения, характеризующие эти способности в нормированном виде. Это означает, что достижения конкретного спортсмена могут быть охарактеризованы не только измеренным результатом  временем пробегания 100 м (t100 ), но и не допускающими прямого измерения способностями (факторами) fi1,fi2,fi3, выраженными в нормированном виде (как отклонение случайных величин от среднего, деленного на стандартное отклонение).

Чем больше факторное значение (по модулю), тем выше (или ниже) проявление скоростной способности у данной спортсменки. Так, например, по способности быстро бегать (фактор 1) лучшим показателем характеризуется спортсменка под № 7 (f71= — 1,74621 ), самый плохой результат у спортсменки под № 4 (f41=1,63124 ). По способности быстро реагировать (фактор 2) лучший показатель демонстрирует спортсменка №9 ( f92=-1,62662), самый плохой результат у спортсменки под № 6 (f62=1,66155 ). По способности быстро набирать скорость (фактор 3) лучший показатель у спортсменки под № 12 (f123 =-2,46242 ), а самый посредственный – у спортсменки под № 10 (f103=1,27179 ), в таблице 4 эти показатели выделены жирным шрифтом.

Таким образом, анализ факторных значений позволяет выявить спортсменок с преимущественным развитием тех или иных способностей.

Таблица 4. — Таблица факторных значений

Дл решения четвертой задачи исследования (определения факторной модели комбинации способностей для достижения результата в беге на 100 м) проанализируем факторные нагрузки, переменной t100 (результат в беге на 100 м), представленные в табл.2. Модель имеет следующий вид:

t100 =-0,875675 fi1+0,303637 fi2+ 0,35638 fi3, где:

t100 – результат в беге на 100 м, представленный в нормированном виде, fi1,gi2, fi3 – выделенные факторы.

Например, результат, показанный спортсменкой, имеющей порядковый номер три, рассчитывается следующим образом (факторные значения берем из табл. 4):

t(3)100= 0,875675_*1,350073 + 0,303637_*1,13503 + 0,35638_*0,17602 =1,58959

Это означает, что результат, показанный спортсменкой № 3 на 1,58 стандартного отклонения больше среднего значения группы исследуемых спортсменок, при этом по способности быстро бегать эта спортсменка отклоняется от средних значений на 1,35 стандартных отклонения, по способности быстро реагировать – на 1,13 стандартных отклонения, по способности быстро набирать скорость на 0,17 стандартных отклонения. Следует учесть, что в беге, чем больше время, тем хуже показанный результат. Следовательно, эта спортсменка показала самый плохой результат. Результаты, представленные в табл.1, свидетельствуют о том, что эта спортсменка действительно показала самый плохой результат в беге на 100 м (14,31 с).

Наоборот, спортсменка, имеющая порядковый номер 7 показала результат, который меньше среднего значения на –1,63 стандартного отклонения, при этом по способности быстро бегать эта спортсменка отклоняется от средних значений на –1,74 стандартных отклонений, по способности быстро реагировать – на 0,6 стандартных отклонения, по способности быстро набирать скорость на –0,81 стандартных отклонения. Следует учесть, что в беге, чем меньше время, тем лучше показанный результат. Результаты, представленные в табл.1, свидетельствуют о том, что эта спортсменка показала лучший результат в беге на 100 м (13,17с). Из модели следует также, что на результат в беге на 100 м в первую очередь влияет способность к быстрому бегу по дистанции (факторная нагрузка равна 0,875675); следующим по степени влияния фактором является способность быстро набирать скорость (факторная нагрузка равна 0,35638). И только третьим – способность быстро реагировать на сигнал (факторная нагрузка равна 0,303637).

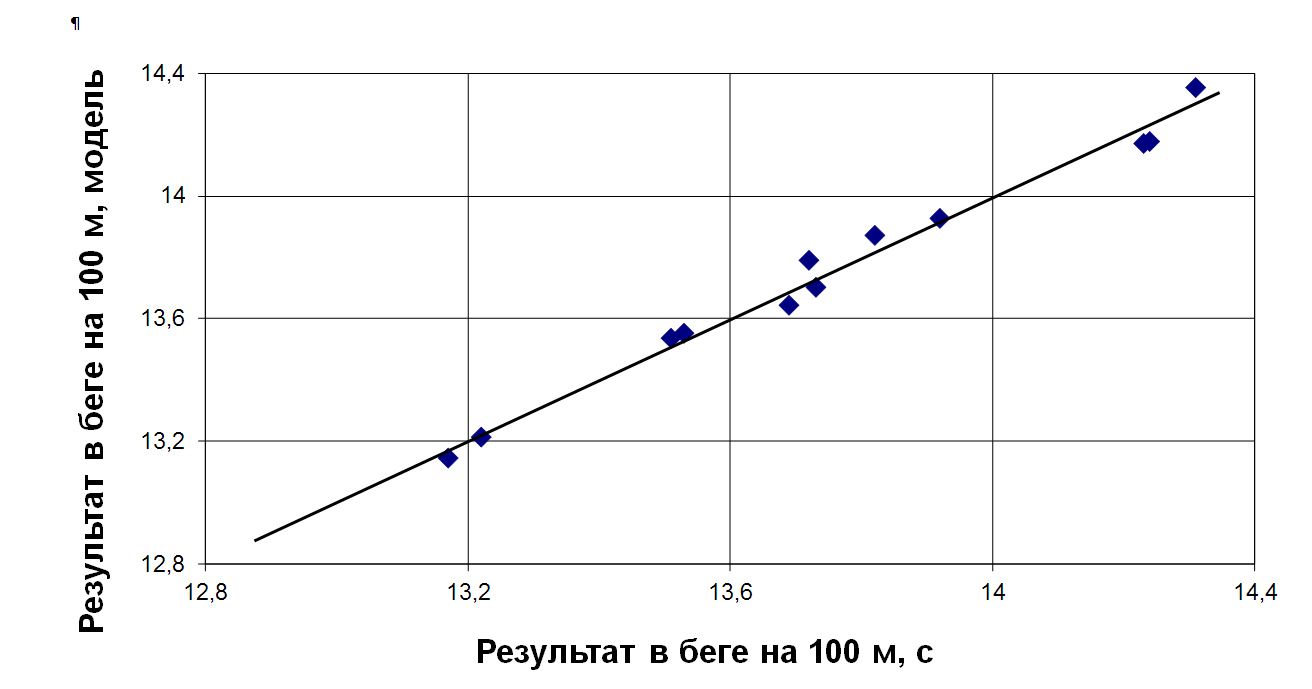
Сопоставление результатов, полученных посредством модели с реальными, зарегистрированными результатами, рис. 3, показало их хорошее соответствие.

ВЫВОДЫ:

1. Факторный анализ позволяет решать ряд важных задач в области физической культуры и спорта, а именно: изучать факторную структуру способностей спортсменов, выявлять информативные тесты для оценки этих способностей, определять спортсменов с преимущественным развитием различных способностей, а также формировать факторную модель комбинации способностей для достижения определенного результата.
2. На конкретном примере из области физической культуры и спорта показана возможность решения этих задач посредством факторного анализа.

ЛИТЕРАТУРА

1. Бююль А, Цефель П. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей.– СПб: Диасофт, СПб 2001.– 608 с.
2. Дюк В. Обработка данных на ПК в примерах.&? СПб: Питер, 1997.– 240 с.
3. Зациорский В.М. Кибернетика, математика, спорт.– М.: Физкультура и спорт, 1969.– 199 с.
4. Масальгин Н.А., Медведев А.С. Многомерный статистический анализ в исследованиях по физиологии спорта //Метод. разработка для аспирантов, преподавателей и слушателей Высшей школы тренеров и факультета усовершенствования.– М., 1991.– 35 с.