
Числовые характеристики выборки (случайной величины)
В.С. Иванов (1990) в книге «Основы математической статистики» пишет: «Вариационные ряды и графики эмпирических распределений дают наглядное представление о том, как варьирует признак в выборочной совокупности. Но они недостаточны для полной характеристики выборки, поскольку содержат много деталей, охватить которые невозможно без обобщающих числовых характеристик. Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой».
Наибольшее практическое значение имеют характеристики положения, рассеивания и асимметрии (табл.1). В конце этой страницы расположен видеофайл, объясняющий как рассчитать числовые характеристики выборки (случайной величины) в пакете STATGRAPHICS.
Таблица 1 — Название и обозначение числовых характеристик выборки (случайной величины)
Числовые характеристики случайной величины | ||
| Положения | Вариативности | Формы распределения |
| Среднее арифметическое (М) | Размах вариации (R) | Коэффициент асимметрии (As) |
| Мода (Мо) | Дисперсия (S2) | Коэффициент эксцесса (Ex) |
| Медиана (Ме) | Стандартное отклонение (S) | — |
Коэффициент вариации (V%) | ||
Характеристики положения
Среднее арифметическое
Среднее арифметическое (М) – одна из основных характеристик выборки. Этот показатель характеризуется тем, что сумма отклонений от него выборочных значений (с учетом знака) равна нулю.
Для вычисления среднего арифметического сумму всех значений признака делим на объем выборки.
Пример: xi : 20, 15, 15, 20, 30, среднее арифметическое равно 20. При этом сумма отклонений вариант от среднего арифметического равна нулю: сумма отклонений= 0 +(-5) + (-5) + 0 + 10 = 0.
М=(20+15+15+20+30)/5=20
Следует заметить, что среднее арифметическое измеряется в тех же единицах, что и признак. Например, если масса человека измеряется в кг, то и среднее арифметическое измеряется в кг.
Среднее арифметическое, вычисленное на основе выборочных данных, то есть данных, полученных на выборке, называется выборочным средним арифметическим. Оно обозначается как М (Mean). Среднее арифметическое генеральной совокупности называется генеральным средним арифметическим. Оно обозначается буквой мю (μ).
Мода
Мода (Мо) – характеристика положения. Представляет собой значение признака, встречающееся в выборке наиболее часто (рис.1).
В качестве примера рассмотрим выборку: xi :3; 3; 3; 5; 5; 3; 4; 6; 7; 5; 3.
В выборке цифра «3» встречается 5 раз, поэтому Мо = 3.
С точки зрения анализа данных, мода несёт информацию о «типичных» значениях признака, а не о наиболее вероятных (как среднее).
Медиана
Медиана (Ме)- характеристика положения, представляет собой такое значение признака, при котором одна половина значений меньше ее, а другая – больше.
В качестве примера рассмотрим выборку: xi :3; 3; 3; 5; 5; 3; 4; 6; 7; 5; 3.
Чтобы легко было определить медиану расположим варианты по возрастанию.
xi :3; 3; 3; 3; 3; 4; 5; 5; 5; 6; 7. Варианта со значением «4» стоит в середине этой выборки. Это и есть медиана.
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта (электронная книга)
- Математическая статистика в спортивных исследованиях (электронная книга)
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
Медиана относится к классу непараметрических статистик. В анализе данных медиана может использоваться как альтернатива среднего арифметического, так как она устойчива к выбросам и аномальным значениям.
Сравнение характеристик положения выборки
Характеристики положения называют также мерами центральной тенденции (Дж. Гласс, Дж. Стенли, 1976). Эти меры по-разному характеризуют выборку (рис. 2).
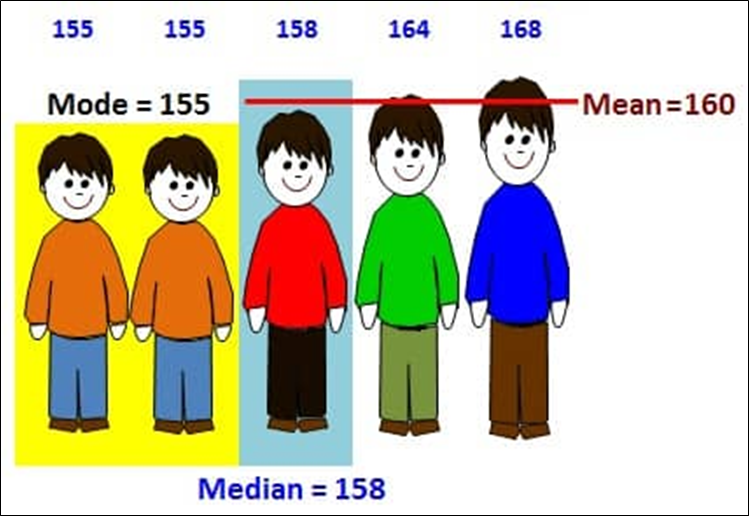
В малых группах мода может быть совершенно нестабильной. Однако для большого объема данных мода является достаточно стабильной характеристикой.
На медиану не влияют большие или малые значения признака. Например, в выборке из 50 объектов, значение медианы не изменится, если наибольшее значение признака утроится.
На значение среднего арифметического очень сильно влияют «выбросы», то есть данные, находящиеся далеко от центра.
Дж. Гласс и Дж. Стенли (1976) приводят следующий анекдот для характеристики проблем, которые связаны с выбором меры центральной тенденции.
Однажды пятеро мужчин сидели рядом на скамейке парка. Двое были бродягами, имущество которых выражалось в 25 центов. Третий был рабочим, чей счет в банке и другое имущество составляли 2000 долларов. Четвертый владел 15000 долларами в разных формах. Пятый же был миллионером с чистым доходом 5 000 000 долларов. Поэтому мода для этой группы равна 25 центам. Эта цифра очень хорошо характеризует двоих, но является чрезвычайно некорректной для трех других. Медиана равна 2000 долларов и хорошо характеризует только рабочего. Среднее в 1003400, 10 долларов не является удовлетворительным даже для миллионера. Очевидно, нет меры центральной тенденции, адекватной этой группе.
В области физической культуры и спорта чаще всего применяются две характеристики: среднее и медиана. Считается, если данные представлены в баллах или распределение признака отличается от нормального для характеристики выборки правильнее применять медиану. Если данные представлены в интервальной шкале или шкале отношений, а также если распределение признака соответствует нормальному, рекомендуется использовать среднее арифметическое.
Характеристики вариативности
Средние значения не дают полной информации о вариации признака, поэтому наряду со средними значениями вычисляют характеристики вариативности.
К этим характеристикам относятся:
- размах вариации признака;
- дисперсия признака (случайной величины);
- стандартное отклонение;
- коэффициент вариации.
Размах вариации признака
Размах вариации признака (R) вычисляется как разность между максимальным и минимальным значением признака:
R= Xmax-Xmin.
Размах вариации признака измеряется в тех же единицах, что и признак. Информативность этого показателя невелика, так как эмпирические распределения результатов могут иметь одинаковый размах варьирования, а их форма будет очень отличаться.
Рассмотрим следующий пример. Имеем оценки, показанные школьниками двух классов:
Class А: 1;2;3;4;5
Class B: 1;5;5;5;5
В этом случае размах вариации признака одинаков и равен: R= Xmax-Xmin =5-1=4.
Однако распределение результатов учеников класса А и Б сильно различается.
Дисперсия признака
Дисперсия признака (S2) – средний квадрат отклонений значений признака от среднего арифметического.
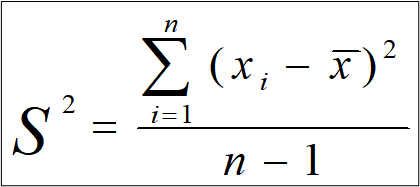
где: xi — значение варианты; x (c чертой) — среднее арифметическое; n — объем выборки.
Иногда вместо дисперсии признака говорят дисперсия выборки или дисперсия случайной величины.
Дисперсия выборки характеризует ее вариативность (рис.3), при этом каждая из вариант вносит свой вклад.
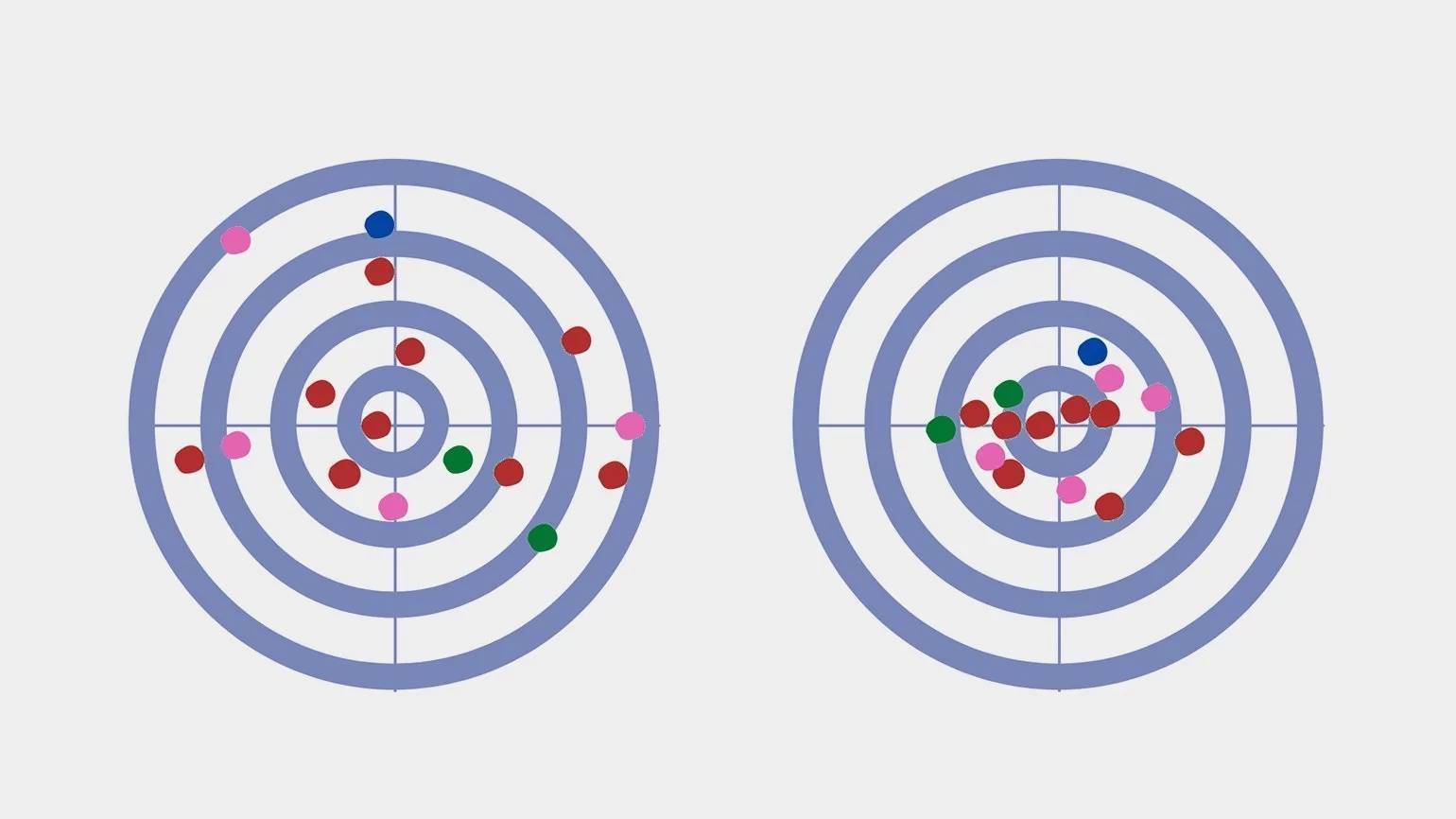
Это отличает дисперсию от размаха вариации, на значение которого влияют только две варианты: минимальное и максимальное значение признака.
Если признак измеряется в метрах, то дисперсия – в м2. Это является недостатком этого показателя, поэтому наиболее часто в публикациях приводится не дисперсия, а стандартное отклонение (S). Этот показатель также называется среднеквадратическим отклонением или СКО.
Стандартное отклонение (S) представляет собой корень квадратный из дисперсии. Чем больше стандартное отклонение, тем больше варьирует признак.
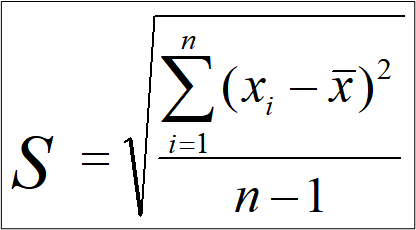
Понятие стандартного отклонения в статистику ввел Карл Пирсон. В отличие от дисперсии стандартное отклонение измеряется в тех же единицах, что и признак.
Рассмотрим, как рассчитывается дисперсия и стандартное отклонение на следующем примере.
Имеем следующие значения признака: 20, 15, 15, 20, 30
Вначале рассчитываем среднее арифметическое (М), оно равно: (20+15+15+20+30)/5=20. Теперь заполняем таблицу 2
Таблица 2 — Cхема расчета дисперсии признака
| n | xi | xi-M | (xi-M)2 |
| 1 | 20 | 0 | 0 |
| 2 | 15 | -5 | 25 |
| 3 | 15 | -5 | 25 |
| 4 | 20 | 0 | 0 |
| 5 | 30 | 10 | 100 |
| Сумма | 150 |
Теперь рассчитываем дисперсию: S2=150/(5-1)=37,5, а стандартное отклонение равно:
S=SQR (37,5)= 6,12.
Коэффициент вариации признака
Чтобы сопоставить вариативность признаков, измеренных в различных единицах, используется относительный показатель (СV%), который называется коэффициентом вариации. Этот коэффициент предложен Карлом Пирсоном.
Коэффициент вариации рассчитывается следующим образом:
СV%=100% (S /M),
где: S — стандартное отклонение; M — среднее арифметическое.
Например, среднее арифметическое роста спортсменок равно М=170 см, а стандартное отклонение S=5 см, тогда коэффициент вариации равен: СV%= 100% (5/170)=2,94.
Коэффициент вариации часто используют для оценки однородности выборки. Если СV<10% – выборка однородна, то есть, получена из одной генеральной совокупности.
Характеристики формы распределения признака
Форма распределения признака характеризуются два показателя:
- коэффициент асимметрии;
- коэффициент эксцесса.
Коэффициент асимметрии
Коэффициент асимметрии (As) характеризует “скошенность“ эмпирического распределения признака (рис. 4).
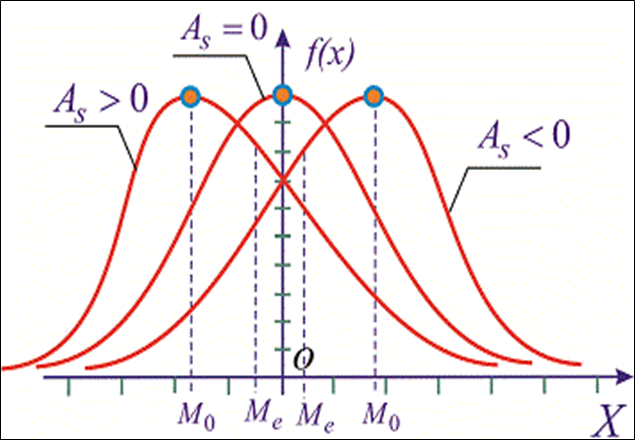
Он рассчитывается по следующей формуле:
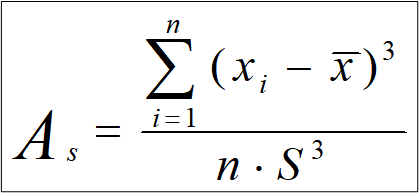
Если коэффициент асимметрии равен нулю, то есть As=0 – распределение симметричное (рис.4). Если коэффициент асимметрии больше нуля, то есть As>0 — вершина распределения скошена влево. Если коэффициент асимметрии меньше нуля то есть As <0 — вершина распределения скошена вправо.
Коэффициент эксцесса
Коэффициент эксцесса (Ex) определяет характер эмпирического распределения: остро- или плосковершинный (рис.5).
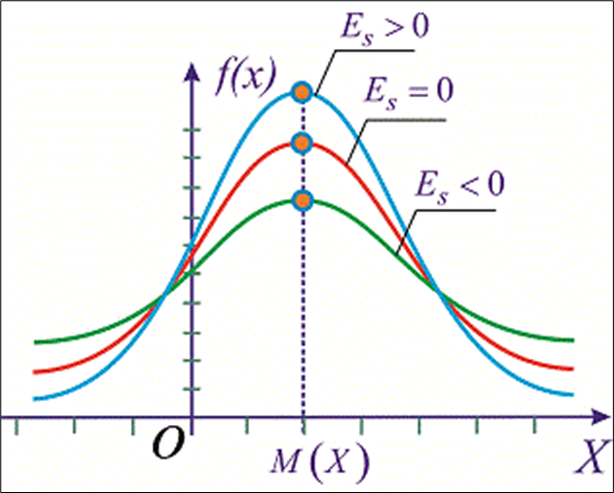
Коэффициент эксцесса рассчитывает по формуле: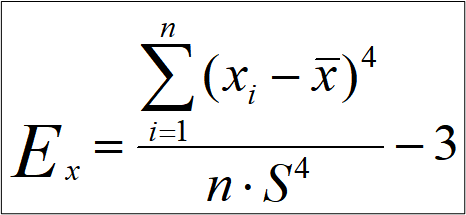 Если распределение соответствует нормальному закону — коэффициент эксцесса равен нулю (рис.7). Если распределение признака плосковершинное — коэффициент эксцесса меньше нуля, то есть Ex<0. Если распределение признака островершинное — коэффициент эксцесса больше нуля, то есть то есть Ex>0.
Если распределение соответствует нормальному закону — коэффициент эксцесса равен нулю (рис.7). Если распределение признака плосковершинное — коэффициент эксцесса меньше нуля, то есть Ex<0. Если распределение признака островершинное — коэффициент эксцесса больше нуля, то есть то есть Ex>0.
Причины асимметрии и эксцесса признака
Причинами асимметрии и эксцесса распределения признака может быть неоднородность выборки. В.М. Зациорский (1969) изучал результаты физической подготовленности студентов г. Москвы и получил следующие результаты (таблица 3).
Таблица 3 — Результаты физической подготовленности студентов г. Москвы
| Показатель | Пол | n | x ̅ | S | A_s | E_x |
| Бег 100 м, с | М | 4812 | 14,2 | 0,87 | 0,53 | 1,11 |
| Прыжок в длину, см | М | 4086 | 4,39 | 0,43 | 0,33 | 1,83 |
Из таблицы 3 следует, что несмотря на большой объем выборки коэффициент эксцесса достаточно большой (больше 1). После того, как были отобраны студенты первого курса, возраста 17-19 лет, которые родились в Москве и не занимались регулярно спортом, было установлено, что коэффициенты эксцесса значительно уменьшились (таблица 4).
Таблица 4 — Результаты физической подготовленности студентов г. Москвы после устранения неоднородности выборки
| Показатель | Пол | n | x ̅ | S | A_s | E_x |
| Бег 100 м, с | М | 217 | 14,0 | 0,51 | 0,51 | 0,21 |
| Прыжок в длину, см | М | 217 | 5,36 | 0,24 | 0,23 | 0,52 |
Также установлено, что засуха вызывает значительную асимметрию в длине колосьев (Лакин Г.Ф., 1980).
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Лакин Г.Ф. Биометрия.- М.: Высшая школа, 1980.- 293 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
- Самсонова, А.В. Математическая статистика в спортивных исследованиях: учебное пособие / А.В. Самсонова, И.Э. Барникова: НГУ им.П.Ф.Лесгафта, Санкт-Петербург.- СПб [б.и.], 2022.- 122 c.
Расчет числовых характеристик одной переменной в Statgraphics:
С уважением, А.В. Самсонова
- Учебные пособия по статистике
- Видеоуроки по Statgraphics
- Введение в математическую статистику
- Генеральная совокупность и выборка
- Статистические шкалы
- Эмпирические распределения
- Числовые характеристики выборки
- Стандартная ошибка среднего арифметического
- Представление результатов исследования
- Точечное и интервальное оценивание числовых характеристик
- Элементы теории вероятностей
- Нормальный закон распределения (закон нормального распределения)
- Статистические гипотезы
- Критерии проверки статистических гипотез
- Критерии согласия
- Обоснование выбора критерия значимости
- Параметрические критерии
- Статистические операции в номинальной шкале
- Представление данных статистического анализа
- Корреляционный анализ
- Представление данных корреляционного анализа
- Регрессионный анализ
- Представление результатов регрессионного анализа