Скалярные и векторные величины
Даны определения и приведены примеры скалярных и векторных величин. Описаны математические операции над векторными величинами.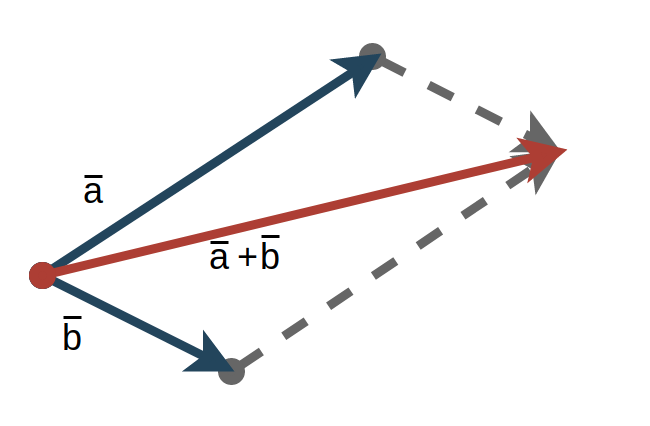
Скалярные и векторные величины в биомеханике
Физические величины бывают скалярными и векторными
Скалярные величины
Скалярная величина (от лат. scalaris – ступенчатый) в механике – величина, каждое значение которой может быть выражено одним числом.
Примеры скалярных величин: масса тела, время, температура, длина, путь, площадь.
Векторные величины
Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. То есть вектор определяется численным значением и направлением.
Примеры векторных величин: перемещение, скорость, ускорение, сила, момент силы, импульс тела.
Обозначение векторных величин
На рисунках и схемах вектор отображается отрезком прямой со стрелкой на одном конце. Длина отрезка в выбранном масштабе выражает числовое значение векторной величины (его модуль), а стрелка указывает ее направление.
На рисунках, схемах и в тексте векторные величины обозначают несколькими способами:
1 способ. Векторная величина обозначается строчной или заглавной буквой со стрелкой или чертой над ней (рис. 1).
2 способ. Векторная величина обозначается заглавными буквами, обозначающими начало и конец вектора с чертой или стрелками над ними (рис. 1).
3 способ. Иногда векторные величины в формулах обозначаются жирным шрифтом, а скалярные — обычным. Например: F=ma
Операции над векторными величинами (векторами)
Над векторными величинами возможны следующие математические операции:
- Сложение и вычитание векторов.
- Умножение вектора на скаляр.
- Произведение векторов (скалярное и векторное).
Литература
- Петров В.А., Гагин Ю.А. Механика спортивных движений. – М: Физкультура и спорт, 1974. – 232 с.
С уважением, А.В. Самсонова