Статистическая обработка результатов эксперимента
Лекция 1. Основные понятия математической статистики
В этом разделе приведены часто используемые термины, необходимые для понимания изложенного материала.
Числовые характеристики выборки – обобщенные показатели, позволяющие:
- дать количественную оценку эмпирическим распределениям;
- сравнивать выборки между собой.
Статистической гипотезой (гипотезой) называется утверждение относительно истинных значений параметров исследуемой генеральной совокупности.
Нулевая гипотеза (Но) – предположение о том, что между параметрами генеральных совокупностей разница равна нулю и различия между ними носят не систематический, а случайный характер.
Альтернативная гипотеза (Н1) – гипотеза, противоположная нулевой.
Уровень значимости — вероятность отклонения нулевой гипотезы, когда она верна или другими словами вероятность ошибки.
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта (электронная книга)
- Математическая статистика в спортивных исследованиях (электронная книга)
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
Критерий — метод проверки статистических гипотез.
Критерий хи-квадрат, критерий лямбда Колмогорова–Смирнова – критерии согласия, часто используемые для проверки гипотезы о нормальности распределения.
t – критерий Стьюдента – критерий, позволяющий оценить, насколько статистически существенно различаются средние арифметические двух выборок.
F – критерий Фишера – метод, позволяющий проверить гипотезу, что две независимые выборки получены из генеральных совокупностей X и Y с одинаковыми дисперсиями sx2 и sY2 .
Критерий Манна-Уитни — непарамтерический критерий проверки статистических гипотез. Применяется для независимых выборок.
Критерий Вилкоксона – непараметрический критерий проверки статистических гипотез. Применяется для связанных выборок.
Корреляционный анализ – метод статистической обработки результатов, сущность которого состоит в определении степени взаимосвязи между двумя случайными величинами X и Y.
Лекция 2. Числовые характеристики выборки
В своей статье, опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь “…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52.
После проведения эксперимента исследователь получает определенные результаты. Чтобы его результаты можно было сравнить с данными других исследователей, необходимо рассчитать числовые характеристики выборки. Наибольшее практическое значение имеют характеристики положения, рассеивания и асимметрии (табл.1).
Таблица 1 — Название и обозначение числовых характеристик выборки
Характеристики | ||
Положения | Вариативности | Формы распределения |
Среднее арифметическое (М) | Размах вариации (R) | Коэффициент асимметрии (As) |
Мода (Мо) | Дисперсия (S2) | Коэффициент эксцесса (Ex) |
Медиана (Ме) | Стандартное отклонение (S) | — |
Характеристики положения
Среднее арифметическое (М) – одна из основных характеристик выборки. Этот показатель характеризуется тем, что сумма отклонений от него выборочных значений (с учетом знака) равна нулю.
где: n – объем выборки, xi – варианты выборки.
Среднее арифметическое, вычисленное на основе выборочных данных, как правило, не совпадает с генеральным средним. Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности (m).
где: S — стандартное отклонение (см. далее).
В научных публикациях очень часто окончательный результат приводится в следующем виде: М±m. В качестве примера приведем фрагмент таблицы из публикации Г.Г.Лапшиной (табл. 2).
Таблица 2 — Антропометрический и функциональный статусы студенток, n= 83 (по: Г.Г.Лапшиной, 1989)
Показатели | М±m | s |
Длина тела, см | 163,7±0,9 | 5,8 |
Масса тела, кг | 60,8±1,2 | 7,5 |
Медианой (Me) – называется такое значение признака, когда одна половина значений экспериментальных данных меньше ее, а вторая половина — больше.
Мода (Мо) – представляет собой значение признака, встречающееся в выборке наиболее часто.
Характеристики вариативности
Средние значения не дают полной информации о варьирующем признаке, поэтому наряду со средними значениями вычисляют характеристики вариации.-
Размах вариации (R) вычисляется как разность между максимальным и минимальным значением признака: R= Xmax-Xmin.
Информативность этого показателя невелика, так как распределения результатов могут иметь одинаковый размах варьирования, а их форма будет очень отличаться.
Дисперсия (S2) – средний квадрат отклонений значений признака от среднего арифметического (4):
Наиболее часто в публикациях приводится не дисперсия, а стандартное отклонение (S). Этот показатель также называется среднеквадратическим отклонением или СКО (5):
Во многих публикациях этот показатель обозначается s, однако мы рекомендуем применять обозначения, используемые в книге В.С. Иванова (1990): S – выборочное стандартное отклонение, сигма – стандартное отклонение генеральной совокупности. В качестве примера приведем фрагмент таблицы из статьи Л.Н. Жданова (1996).
Таблица 3 — Зависимость возраста достижения лучшего результата и количество необходимого для этого времени от возраста начала спортивной специализации у конькобежцев, дистанция 500 м, 225 спортсменов (по: Л.Н.Жданову, 1996).
Возраст начала спортивной специализации, лет | Спортивная квалификация | Мальчики, юноши | ||
Возраст лучшего результата | Количество лет с начала специализации | |||
М | S | |||
10 | МC | 20,0 | 0,5 | 10,0 |
КМС | 17,6 | 0,5 | 7,6 | |
I,II | 15,0 | 0,3 | 5,0 | |
Коэффициент вариации (V%). Чтобы сопоставить вариативность признаков, измеренных в различных единицах, используется относительный показатель (6), которы йназывается коэффициентов вариации.
Коэффициент вариации используют для оценки однородности выборки. Если V < 10% – выборка однородна, то есть, получена из одной генеральной совокупности. Очень часто в публикациях приводят четыре показателя: объем выборки, среднее арифметическое, стандартное отклонение и коэффициент вариации (К.А.Ежевская, 1995).
Характеристики асимметрии
Коэффициент асимметрии (As) характеризует “скошенность“ эмпирического распределения.
Коэффициент эксцесса (Ex) определяет характер эмпирического распределения: остро- или плосковершинный.
Лекция 3. Закон нормального распределения
Корректное использование критериев проверки статистических гипотез предполагает знание закона распределения. Так, например, использование t – критерия Стьюдента и F-критерия Фишера требует нормального распределения экспериментальных данных. К сожалению, многие исследователи это не учитывают.
Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения. График плотности вероятности нормального распределения имеет следующий вид (рис. 1).
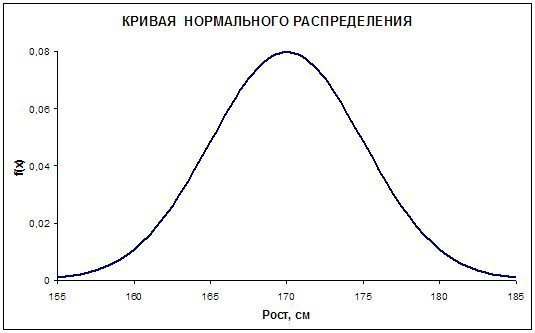
На рис. 1 представлено распределение роста женщин с параметрами: мю (генеральное среднее) – 170 см, s = 5 см.
Нормальное распределение обладает следующими свойствами:
1. Нормальная кривая имеет колокообразную форму, симметричную относительно x = мю.
2. Точки перегиба отстоят от мю на ± сигма .
3. Нормальное распределение полностью определяется двумя параметрами: мю и сигма.
4. Медиана и мода совпадают и равны мю.
5. В интервал мю ± сигма попадают 68 % всех результатов.
В интервал мю ± 2 сигмы попадают 95% всех результатов.
В интервал мю ± 3 сигмы попадают 99 % всех результатов.
Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов. Можно использовать свойства нормального распределения (равенство среднего, моды и медианы). Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:
если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки;
если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова;
Лекция 4. Проверка статистических гипотез
Рассчитав числовые характеристики выборки, экспериментатор получает возможность сравнивать свои результаты с данными других исследователей или сравнить результаты, показанные контрольной и экспериментальной группой. Иногда задача работы состоит в том, чтобы сравнить результат, показанный группой спортсменов до и после эксперимента. В этом случае, чтобы дать ответ, существуют ли достоверные различия в результатах, нужно проверить статистические гипотезы, использовав для этого специальные методы — критерии значимости. Таким образом, критерий значимости — это метод проверки статистической гипотезы.
При использовании критериев значимости выдвигается нулевая гипотеза (Ho) — предположение о том, что в параметрах генеральных совокупностей из которых получены данные, представленные в выборках, разница равна нулю и различия между ними носят не систематический, а случайный характер. Противоположная гипотеза называется альтернативной (Н1).
Для проверки статистических гипотез применяются параметрические и непараметрические критерии. Параметрические критерии включают в формулу расчета параметры распределения, в нашем случае нормального. поэтому первым условием использования параметрических критериев является нормальное распределение результатов исследования. Вторым условием применения параметрических критериев является статистическая шкала, в которой представлены данные. Такими шкалами являются интервальная шкала и шкала отношений (данные, представлены в этих шкалах измеряются в кг, м, с и т.д). Непараметрические критерии (или ранговые критерии) построены по другому принципу и не требуют нормального распределения экспериментальных результатов. Кроме того, эти критерии можно применять к данным, представленным в порядковой шкале (баллы).
Параметрические критерии
К параметрическим критериям относят: критерий Стьюдента для независимых выборок и критерий Стьюдента для связанных выборок.
t–критерий Стьюдента для независимых выборок
Условия применения: обе выборки независимы и получены из генеральных совокупностей X и Y, имеющих нормальное распределение с параметрами μx , μy , σx σy .
Гипотеза: Ho: μx= μy (предполагается равенство средних арифметических генеральных совокупностей).
Альтернатива: H1: μx ≠ μy или H1 μx >μy или H1: μx<μy (в зависимости от того, что требуется доказать: простое различие средних или то, что одно из них больше другого).
t – критерий Стьюдента рассчитывается по формуле (1):
|mx— my|/ S x-y (1)
Значение S x—y зависит от того, равны или не равны объемы выборки, а также их дисперсии.
В случае равенства дисперсий и объемов выборок S x-y вычисляются по формуле (8)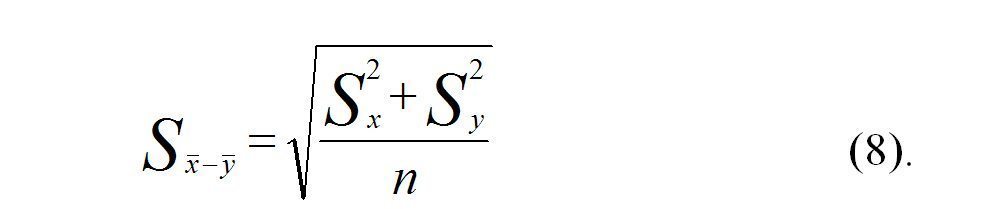
t–критерий Стьюдента для связанных выборок (парные сравнения)
В практике педагогических исследований часто используются так называемые парные сравнения (до и после эксперимента). При парных сравнениях нельзя использовать рассмотренные выше методы для независимых выборок, поскольку это приведет к большим ошибкам. Для сравнения средних значений нужно использовать модификацию t – критерия Стьюдента для связанных выборок. Особенность расчета t – критерия в том, что гипотеза формулируется в отношении разностей сопряженных пар наблюдений.
Условия применения: di = xi – yi – разность связанных пар результатов измерения. Делается предположение о нормальном распределении этих разностей в генеральной совокупности с параметрами md , sd.
Гипотеза: Ho: md =0.
Альтернатива: H1: md ¹ 0 или H1: md > 0 или H1: md < 0.
Значение t – критерия Стьюдента определяется по формуле (10):
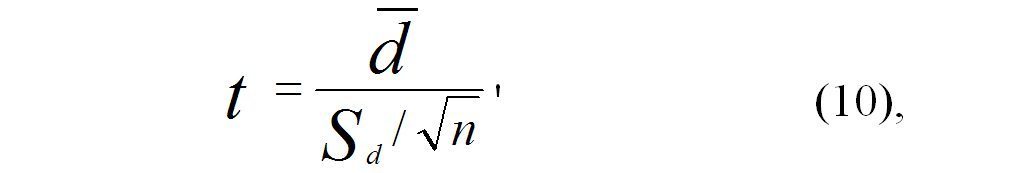
где: `d – среднее арифметическое разностей, Sd` стандартное отклонение.
Непараметрические критерии
Применение параметрических критериев (t – критерия Стьюдента) связано с целым рядом допущений. Например, сравнивая выборочные средние значения с помощью t – критерия Стьюдента, принимались следующие предположения: обе выборки являются случайными, то есть каждая из них получена в результате независимых измерений, обе выборки получены из генеральных совокупностей, имеющих нормальное распределение, дисперсии генеральных совокупностей равны между собой. На практике эти предположения строго никогда не выполняются, поэтому применение параметрических критериев всегда связано с опасностью ошибочных выводов, возникающих из-за нарушения принятых допущений. В последнее время в математической статистике интенсивно разрабатываются непараметрические методы, которые строятся так, чтобы их применение зависело от возможно меньшего числа допущений.
Параметрические критерии применимы только для сравнения выборочных данных, представляющих собой результаты измерений, выраженных в единицах метрических шкал (метры, килограммы, секунды и т.д.). Но в спортивных исследованиях часто приходится иметь дело с данными, выраженными в шкалах порядка, например, произвольная нумерация игроков в команде, места, занятые спортсменами в соревнованиях и т.д. Такие данные нельзя сравнивать с помощью параметрических критериев, а непараметрические критерии могут быть успешно применены и к данным этого типа.
Сравнение двух независимых выборок (критерий Манна-Уитни для независимых выборок)
Условие применения. Применение критерия Вилкоксона основано на единственном предположении: выборки получены из однотипных непрерывных распределений. При этом вид распределения генеральных совокупностей никак не оговаривается.
Гипотеза: Ho: Mex = Mey (предполагается равенство медиан двух генеральных совокупностей).
Альтернатива: H1: Mex ¹ Mey или H1: Mex > Mey или H1: Mex < Mey (в зависимости от того, что требуется доказать: простое различие медиан или то, что результаты в экспериментальной группе больше чем в контрольной).
Сравнение двух связанных выборок (критерий Вилкоксона для связанных выборок)
Гипотеза: Ho: Med = 0
Альтернатива: H1: Med ¹ 0 или H1: Med > 0 или H1: Med < 0
Порядок использования t – критерия Стьюдента и W – критерия Вилкоксона следующий. При обработке выборочных данных рассчитывается фактическое значение критерия. Затем по табличным данным определяется его критическое значение. Если фактическое значение меньше, чем критическое на уровне значимости α=0,05, то различие считается статистически незначимым (р>0,05). Если вычисленное по выборке значение критерия превышает критические значения при a=0,05; a=0,01 или a=0,001, то различия считаются статистически значимыми. Это записывается следующим образом: p<0,05; p<0,01; p<0,001. В качестве примера рассмотрим таблицу 4.
Таблица 4 — Изменение высоты прыжка верх с места после силовых и скоростно-силовых тренировок в макроцикле (по: В.В.Марченко, Л.С.Дворкину, В.Н.Рогозяну, (1998).
Макроциклы | Силовая тренировка Высота прыжка, см | Стат. вывод | Скоростно-силовая тренировка Высота прыжка, см | Стат вывод | ||
до | после | до | после | |||
1 | 53 ±1,4 | 50±1,4 | р<0,001 | 54±1,3 | 54±1,3 | р>0,05 |
2 | 63±0,8 | 58±1,4 | р<0,001 | 63±0,9 | 63±0,9 | р>0,05 |
3 | 69±1 | 64±1,8 | р<0,01 | 69±1,4 | 70±1,4 | р>0,05 |
Из данных, представленных в таблице 4 следует, что в результате силовой тренировки произошло статистически достоверное уменьшение результатов, показанных спортсменами в прыжке в высоту во всех макроциклах тренировки (p<0,01 и p<0,001). При скоростно-силовой подготовке статистически достоверных изменений в результатах прыжка в высоту не обнаружено (p>0,05).
Лекция 5. Корреляционный анализ
Корреляционный анализ – раздел математической статистики, исследующий зависимости между двумя или более случайными величинами. Термин «Correlation» означает взаимосвязь, взаимоотношение.
Две случайные величины X и Y могут быть:
- связаны функциональной зависимостью (жестко, как зависимость переменных в математическом анализе);
- независимыми;
- связаны стохастической (вероятностной зависимостью) при которой изменение одной величины влечет изменение распределения другой.
В качестве меры связи используется коэффициент корреляции.
Коэффициент корреляции Пирсона (r)
Условия применения:
- Данные представлены в интервальной шкале или шкале отношений.
- Распределение экспериментальных данных подчиняется нормальному закону.
- Предполагается линейная зависимость между случайными величинами X и Y.
Коэффициент корреляции Спирмена (rS)
Условия применения:
- Данные представлены в порядковой, интервальной шкале или шкале отношений.
- Любой закон распределения случайных величин X и Y.
- Между случайными величинами X и Y существует монотонно-возрастающая или монотонно-убывающая зависимость.
Значение коэффициента корреляции находится в пределах от –1 до +1. Если r = +1 или r = –1, то между случайными величинами X и Y существует линейная функциональная зависимость. Если r = 0, то между случайными величинами X и Y отсутствует корреляция, и они называются некоррелированными. Чаще всего величина коэффициента корреляции заключена в границах –1< r < 1. Например, если r=0,898 говорят о положительной корреляции между X и Y, если r=–0,679, говорят об отрицательной корреляции между X и Y.
Очень важно указывать значимость коэффициента корреляции. Например, в эксперименте участвовало 10 человек. Оценивалась взаимосвязь между результатами в беге на 30 м и 100 м. Получен коэффициент корреляции r = 0,611. Чтобы оценить значимость коэффициента корреляции нужно сравнить его с критическим, величина которого зависит от объема выборки и уровня значимости. Если фактическое значение коэффициента корреляции больше, чем критическое, это означает, что коэффициент корреляции достоверен. В нашем случае критическое значение коэффициента корреляции при a = 0,05 составляет r0,05 =0,632. Из этого следует, что рассчитанный коэффициент корреляции статистически недостоверен. Приводить его в своих исследованиях нежелательно.
Таблица 5 — Критические значения коэффициента корреляции Пирсона
| n | 0,05 | 0,01 | 0,001 |
| 3 | 0,9969 | 0,999877 | 0,99999877 |
| 4 | 0,950 | 0,9900 | 0,9990 |
| 5 | 0,878 | 0,9597 | 0,99114 |
| 6 | 0,811 | 0,9172 | 0,9741 |
| 7 | 0,754 | 0,875 | 0,9509 |
| 8 | 0,707 | 0,834 | 0,9244 |
| 9 | 0,666 | 0,798 | 0,898 |
| 10 | 0,632 | 0,765 | 0,872 |
| 20 | 0,444 | 0,561 | 0,679 |
| 30 | 0,361 | 0,463 | 0,570 |
| 40 | 0,312 | 0,402 | 0,501 |
| 50 | 0,279 | 0,361 | 0,451 |
В итоговой таблице необходимо указать объем выборки, чтобы читающий мог оценить значимость (достоверность) вычисленных коэффициентов корреляции. Иногда в публикациях приводятся только значимые коэффициенты корреляции, а вместо незначимых ставится прочерк. В таблице 4 авторы указали, что объем выборки равен n = 32. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (В.С.Иванов, 1990). Следовательно, все коэффициенты корреляции достоверны.
Таблица 6 — Значения коэффициентов корреляции между результатами в скоростно-силовых тестах и результатом в толкании ядра с разгоном n=32, спортивный результат группы варьировал от 12,00 м до 20,50. (по: Я.Е.Ланка, Ан.А.Шалманов, 1982).
Упражнение | 1 | 2 | 3 | 4 | 5 | 6 | |
Толкание ядра с разгона | 1 | 0,97 | 0,84 | 0,83 | 0,73 | 0,73 | |
Толкание ядра с места | 1 | 0,84 | 0,82 | 0,74 | 0,76 | ||
Бросок ядра назад | 1 | 0,85 | 0,71 | 0,66 | |||
Бросок ядра вперед | 1 | 0,66 | 0,62 | ||||
Приседание со штангой | 1 | 0,58 | |||||
Жим штанги лежа | 1 |
Литература
- Боровиков В.П., Боровиков И.П. STATISTICA Статистический анализ и обработка данных в среде Windows.– М.: Филинъ, 1995.– 608 с.
- Дюк В. Обработка данных на ПК в примерах.– СПб: Питер, 1997.– 240 с.
- Ежевская К.А. Особенности динамики показателей скоростных способностей детей 4-6 лет в условиях стандартной тестовой тренировочной программы в детском саду //Теория и практика физической культуры, 1995.– № 3 .–С.15-18.
- Жданов Л.Н. Возраст спортивных достижений //Теория и практика физической культуры, 1996.– № 6 .– С. 59-60.
- Зациорский В.М. Осторожно: статистика! // Теория и практика физической культуры, 1989.– № 2.– С. 52-55.
- Катранов, А.Г. Компьютерная обработка данных экспериментальных исследований / А.Г. Катранов, А.В. Самсонова /Учебное пособие.– СПб: СПбГАФК им. П.Ф. Лесгафта, 2005.– 132 с.
- Ланка Я.Е., Шалманов Ан. А. Биомеханика толкания ядра. – М: Физкультура и спорт, 1982.- 72 с.
- Лапшина Г.Г. Особенности физического состояния студенток гуманитарного факультета // Теория и практика физической культуры, 1989.–№ 4.– С. 18-20
- Марченко В.В., Дворкин Л.С., Рогозян В.Н. Анализ силовой подготовки тяжелоатлета в нескольких макроциклах //Теория и практика физической культуры, 1998.– № 8.– С. 18–22.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ./ /Под ред. В.С.Иванова. М.: Физкультура и спорт, 1990.– 176 с.
- Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере.– М.: Финансы и статистика, 1995.– 384 с.
- Лекции по Математической статистике в ФКиС
- Шаблоны контрольных работ