Деформация растяжение-сжатие материала

Даны определения деформации растяжение-сжатие, механического напряжения, абсолютной и относительной деформации материала. Введено понятие модуля Юнга (модуля продольной упругости, модуля нормальной упругости). Приведены значения модуля Юнга некоторых материалов и элементов ОДА человека.

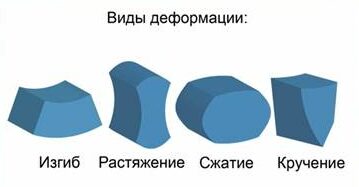
Деформация растяжение-сжатие элементов ОДА человека

Рассматривая понятие механического напряжения, были описаны способы деформирования тела, в результате которого возникает его деформация. В этой записи мы рассмотрим, как происходит деформация по типу «растяжение-сжатие» на примере упругой деформации стержня.

Деформация растяжение-сжатие в сопротивлении материалов – вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (рис. 1).

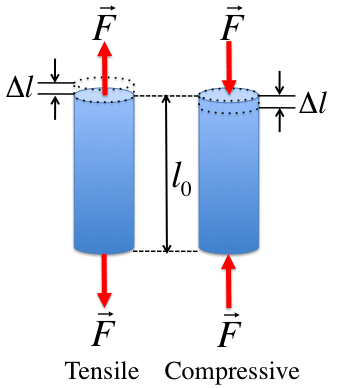
Механическое напряжение, возникающее в стержне при растяжении или сжатии

Рассмотрим следующий пример. Имеем стержень, первоначальная длина которого равна l, а площадь поперечного сечения – S. Если к стержню приложить силу F, направленную перпендикулярно поверхности поперечного сечения (то есть вдоль длинной оси стержня), то в результате этого в нем возникнет механическое напряжение (σ).

Механическое напряжение, возникающее в стержне равно отношению прикладываемой силы F к площади поперечного сечения бруска или стержня: σ=F/S. Оно измеряется в Паскалях [Па].

Абсолютная и относительная деформация тела

Под действием приложенной силы F длина стержня может увеличиться или уменьшится на некоторую величину Δl. Эта величина называется абсолютной деформацией тела (в данном случае – стержня). Так как величина абсолютной деформации тела зависит от первоначальной его длины, степень деформации выражают через отношение абсолютной деформации Δl к первоначальной длине. Это отношение называется относительной деформацией тела (ε). То есть ε= Δl/l. Относительная деформация тела величина безразмерная. Иногда ее выражают в процентах:

ε= (Δl/l) 100%.

Модуль Юнга

Если относительная деформация тела небольшая, связь между нею и механическим напряжением, возникающим в теле, выражается законом Гука:

σ =Е ε,

где Е – коэффициент, численно равный механическому напряжению, которое увеличивает длину образца в два раза. Этот коэффициент ввел в физику английский физик XIX века Томас Юнг.

Модуль Юнга (синонимы: модуль продольной упругости, модуль нормальной упругости) — физическая величина, характеризующая способность материала (тела) сопротивляться растяжению или сжатию при упругой деформации.

Чем больше модуль Юнга, тем больше сопротивление материала растяжению или сжатию при упругой деформации. В табл.1 представлены значения некоторых материалов и элементов ОДА человека. Из таблицы 1 следует, что из представленных в ней материалов наибольший модуль Юнга у стали, наименьший — у резины. Из элементов ОДА человека наибольший модуль Юнга у бедренной кости. Он практически равен показателям железного дерева.

Таблица 1. Модуль упругости (Модуль Юнга) некоторых материалов и элементов ОДА человека

Установлено, что под влиянием силовой тренировки модуль Юнга сухожилия четырехглавой мышцы бедра возрастает с 1300 до 2200 МПа.

Литература

1. Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В.И. Анурьев; 8-е изд., перераб. и доп. Под ред. И.Н. Жестковой. – М.: Машиностроение, 2001. — С. 34.
2. Дубровский В.И., Федорова В.Н. Биомеханика. Учебник: М.: ВЛАДОС-ПРЕСС, 2003. – 672 с.
3. Ершова А.И. Модули упругости и твердость кортикальной костной ткани: наноиндентирование образца бедренной кости // 75-я научная конференция студентов и аспирантов Белорусского государственного университета [Электронный ресурс] : материалы конф. В 3 ч. Ч. 1, Минск, 14–23 мая 2018 г. / Белорус. гос. ун-т, Гл. упр. науки ; редкол.: В. Г. Сафонов (пред.) [и др.]. – Минск : БГУ, 2018. – С. 14-18.
4. Терегулов Ю.Э., Маянская С.Д., Терегулова Е.Т. Изменения эластических свойств артерий и гемодинамические процессы // Практическая медицина, № 2, 2017.- С. 14-20.

С уважением, А.В.Самсонова